题目内容
17.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+2x,x≥0}\\{2x-{x}^{2},x<0}\end{array}\right.$,若f(3-m2)<f(2m),则实数m的取值范围是( )| A. | (-∞,-1) | B. | (3,+∞) | C. | (-∞,-3)∪(1,+∞) | D. | (-∞,-1)∪(3,+∞) |
分析 作出函数f(x)的图象,确定函数的单调性,利用函数的单调性进行求解即可.
解答  解:作出函数f(x)的图象如图,则函数f(x)为增函数,
解:作出函数f(x)的图象如图,则函数f(x)为增函数,
若f(3-m2)<f(2m),
则3-m2<2m,
即m2+2m-3>0,
解得m>1或m<-3,
即实数m的取值范围是(-∞,-3)∪(1,+∞),
故选:C.
点评 本题主要考查函数单调性的应用,根据条件结合图象判断函数的单调性是解决本题的关键.

练习册系列答案
相关题目
2.函数y=Asin(ωx+φ)(ω>0)在一个周期内的图象如图所示,则ω的值是( )
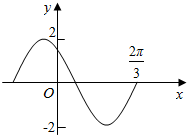

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
6.已知y=f(x)是(0,+∞)上的可导函数,满足(x-1)[2f(x)+xf′(x)]>0(x≠1)恒成立,f(1)=2,若曲线f(x)在点(1,2)处的切线为y=g(x),且g(a)=2016,则a等于( )
| A. | -500.5 | B. | -501.5 | C. | -502.5 | D. | -503.5 |
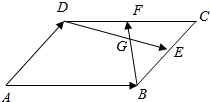 如图所示,?ABCD中,E、F分别是BC、DC的中点,BF与DE交于点G,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.
如图所示,?ABCD中,E、F分别是BC、DC的中点,BF与DE交于点G,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$. 已知椭圆C经过点($\sqrt{3}$,$\frac{1}{2}$)和点($\sqrt{2}$,-$\frac{\sqrt{2}}{2}$),互相垂直的两条射线OA,OB交椭圆C于A,B两点,其中A在第二象限内(如图所示),若D是椭圆的左顶点且BD∥OA.
已知椭圆C经过点($\sqrt{3}$,$\frac{1}{2}$)和点($\sqrt{2}$,-$\frac{\sqrt{2}}{2}$),互相垂直的两条射线OA,OB交椭圆C于A,B两点,其中A在第二象限内(如图所示),若D是椭圆的左顶点且BD∥OA.