题目内容
13.设点P(x,y)为圆x2+y2=1上任-点.求下列两个式子的取值范围.(1)$\frac{y-2}{x+1}$;
(2)x2+y2-2x+6y+1.
分析 (1)设$\frac{y-2}{x+1}=k$,得到kx-y+k+2=0,然后,利用圆心到直线的距离,确定其取值范围;
(2)设z=x2+y2-2x+6y+1=(x-1)2+(y+3)2-9.则z的几何意义圆上的点到定点A(1,-3)距离的平方减9,根据距离公式即可求出z的取值范围.
解答  解:(1)设$\frac{y-2}{x+1}=k$,即kx-y+k+2=0,
解:(1)设$\frac{y-2}{x+1}=k$,即kx-y+k+2=0,
圆心到直线的距离为d=$\frac{|k+2|}{\sqrt{1+{k}^{2}}}$≤1,
∴k≤-$\frac{3}{4}$,
∴$\frac{y-2}{x+1}$的取值范围:($-∞,-\frac{3}{4}$].
(2)令=x2+y2-2x+6y+1=(x-1)2+(y+3)2-9.
可得(x-1)2+(y+3)2=z+9,
表达式(x-1)2+(y+3)2的最值就是圆的圆心与定点A(1,-3)的距离的平方,
|PA|min=$\sqrt{(0-1)^{2}+(0+3)^{2}}$-1=$\sqrt{10}$-1,
z的最小值为:${(\sqrt{10}-1)}^{2}-9$=2-2$\sqrt{10}$,
z的最大值为:${(\sqrt{10}+1)}^{2}-9$=2+2$\sqrt{10}$,
x2+y2-2x+6y+1的取值范围:[2-2$\sqrt{10}$,2+2$\sqrt{10}$].
点评 本题主要考查直线与圆的位置关系的判断,圆的方程的综合应用,根据函数的几何意义是解决本题的关键.

练习册系列答案
相关题目
3.$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$能构成空间的-个基底的条件是( )
| A. | O,A,B,C四点任意三点不共线 | B. | O,A,B,C四点不共面 | ||
| C. | A,B,C三点共线 | D. | 存在实数x,y,z,使x $\overrightarrow{OA}$+y$\overrightarrow{OB}$+z$\overrightarrow{OC}$=$\overrightarrow{0}$ |
2.函数y=Asin(ωx+φ)(ω>0)在一个周期内的图象如图所示,则ω的值是( )
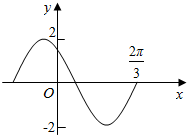

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
9.将夏令营的500名学生分别编号为001,002,…,500,这500名学生分住在三个营区,从001到200在第一营区,从201到350在第二营区,从351到500在第三营区.若采用分层抽样的方法抽取一个容量50的样本,则三个营区被抽取的人数分别为( )
| A. | 20,15,15 | B. | 20,16,14 | C. | 12,14,16 | D. | 21,15,14 |