题目内容
【题目】已知椭圆![]() :
: ![]() 过点
过点![]() ,点
,点![]() ,
, ![]() 是椭圆上异于长轴端点的两个点.
是椭圆上异于长轴端点的两个点.
(1)求椭圆![]() 的离心率;
的离心率;
(2)已知直线![]() :
: ![]() ,且
,且![]() ,垂足为
,垂足为![]() ,
, ![]() ,垂足为
,垂足为![]() ,若
,若![]() 且
且![]() ,求
,求![]() 中点的轨迹方程.
中点的轨迹方程.
【答案】(1) ![]() ;(2) 点
;(2) 点![]() 的轨迹方程为
的轨迹方程为![]() (
(![]() ).
).
【解析】试题分析:(1)点![]() 带入椭圆方程,解得
带入椭圆方程,解得![]() ,易得椭圆
,易得椭圆![]() 的离心率;(2)由
的离心率;(2)由![]() ,且
,且![]() ,易得:
,易得: ![]() .分类讨论直线AB的斜率情况,
.分类讨论直线AB的斜率情况,
联立椭圆方程,易得: ![]() ,借助韦达定理,易得
,借助韦达定理,易得![]() (
(![]() ).
).
试题解析:
(1)依题意, ![]() ,解得
,解得![]() ,
,
故椭圆![]() 的方程为
的方程为![]() ,则其离心率为
,则其离心率为![]() .
.
(2)设直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,
, ![]() ,
, ![]() ,
,
由于![]() ,即
,即![]() ,且
,且![]() ,
,
得![]() ,
, ![]() (舍去)或
(舍去)或![]() ,
,
即直线![]() 经过点
经过点![]() ,设
,设![]() ,
, ![]() ,
, ![]() 的中点
的中点![]() ,
,
①直线![]() 垂直于
垂直于![]() 轴时,则
轴时,则![]() 的重担为
的重担为![]() ;
;
②直线![]() 与
与![]() 轴不垂直时,设
轴不垂直时,设![]() 的方程为
的方程为![]() ,则
,则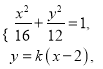
整理得![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
消去![]() ,整理得
,整理得![]() (
(![]() ).经检验,点
).经检验,点![]() 也满足此方程.
也满足此方程.
综上所述,点![]() 的轨迹方程为
的轨迹方程为![]() (
(![]() ).
).

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
【题目】已知某产品的历史收益率的频率分布直方图如图所示:
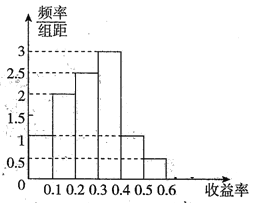
(1)试计算该产品收益率的中位数;
(2)若该产品的售价![]() (元)与销量
(元)与销量![]() (万件)之间有较强线性相关关系,从历史销售记录中抽样得到如表5组
(万件)之间有较强线性相关关系,从历史销售记录中抽样得到如表5组![]() 与
与![]() 的对应数据:
的对应数据:
售价 | 25 | 30 | 38 | 45 | 52 |
销量 | 7.5 | 7.1 | 6.0 | 5.6 | 4.8 |
据此计算出的回归方程为![]() ,求
,求![]() 的值;
的值;
(3)若从上述五组销量中随机抽取两组,求两组销量中恰有一组超过6万件的概率.
【题目】对甲、乙的学习成绩进行抽样分析,各抽五门功课,得到的观测值如表:
甲 | 60 | 80 | 70 | 90 | 70 |
乙 | 80 | 60 | 70 | 80 | 75 |
问:甲、乙谁的平均成绩较好?谁的各门功课发展较平衡?( )
A.甲的平均成绩较好,乙的各门功课发展较平衡
B.甲的平均成绩较好,甲的各门功课发展较平衡
C.乙的平均成绩较好,甲的各门功课发展较平衡
D.乙的平均成绩较好,乙的各门功课发展较平衡