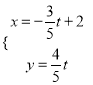题目内容
【题目】已知y=f(x)是偶函数,而y=f(x+1)是奇函数,且对任意0≤x≤1,都有f(x)≥0,f(x)是增函数,则a=f(2010),b=f( ![]() ),c=﹣f(
),c=﹣f( ![]() )的大小关系是( )
)的大小关系是( )
A.b<c<a
B.c<b<a
C.a<c<b
D.a<b<c
【答案】A
【解析】解答:∵y=f(x)是偶函数,而y=f(x+1)是奇函数,∴4为函数的一个周期,
又∵对任意0≤x≤1,都有f(x)≥0,
∴a=f(2010)=f(2)=﹣f(0)
b=f( ![]() )=﹣f(
)=﹣f( ![]() ),
),
c=﹣f( ![]() )
)
∵0< ![]() <
< ![]() <1
<1
∴f( ![]() )>f(
)>f( ![]() )>f(0)
)>f(0)
∴b<c<a
故选A
分析:y=f(x)是偶函数,而y=f(x+1)是奇函数可推断出=f(x)是周期为4的函数,y=f(x)是偶函数,对任意0≤x≤1,都有f(x)≥0,f(x)是增函数,由这些性质将三数化简为自变量在0≤x≤1的函数值来表示,再利用单调性比较大小.
【考点精析】利用奇偶性与单调性的综合对题目进行判断即可得到答案,需要熟知奇函数在关于原点对称的区间上有相同的单调性;偶函数在关于原点对称的区间上有相反的单调性.

练习册系列答案
相关题目
【题目】海南中学对高二学生进行心理障碍测试得到如下列联表:
焦虑 | 说谎 | 懒惰 | 总计 | |
女生 | 5 | 10 | 15 | 30 |
男生 | 20 | 10 | 50 | 80 |
总计 | 25 | 20 | 65 | 110 |
试说明在这三种心理障碍中哪一种与性别关系最大?
参考数据:K2= ![]()
P(K2≥k) | 0.5 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.535 | 7.879 | 10.828 |