Question

【题目】如图,矩形ABCD所在的平面与平面AEB垂直,且∠ BAE=120°,AE=AB=4,AD=2,F,G,H分别为BE,AE,BC的中点.

(1)求证:直线DE与平面FGH平行;

(2)若点P在直线GF上,且二面角D-BP-A的大小为,试确定点P的位置.

Answer 1

【答案】（1）见解析；（2）见解析

【解析】

取AD中点M，易得M在平面FHG。另一方面，MG∥DE。故直线DE与平面FGH平行

以A为坐标原点。建立合适的坐标系，设=λ=(0,2λ,0),求出平面PBD的一个法向量n1=(5-2λ,,2)。又平面ABP的一个法向量为n2=(0,0,1),又cos<n1,n2>=,即可得出λ的值。进而可求出P点坐标。

(1)证明取AD的中点M,连接MH,MG.

∵G,H分别是AE,BC的中点,

∴MH∥AB,GF∥AB,∴M∈平面FGH.

又MG∥DE,且DE平面FGH,MG平面FGH,

∴DE∥平面FGH.

(2)如下图

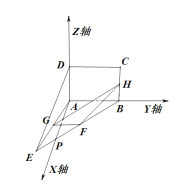
在平面ABE内,过A作AB的垂线,记为AP,则AP⊥平面ABCD.

以A为原点,AP,AB,AD所在的直线分别为x轴,y轴,z轴建立空间直角坐标系A-xyz.

所以A(0,0,0),B(0,4,0),D(0,0,2),E(2,-2,0),G(,-1,0),F(,1,0).

则=(0,2,0),=(0,-4,2),=(,-5,0).

设=λ=(0,2λ,0),

则=(,2λ-5,0).

设平面PBD的法向量为n1=(x,y,z),

则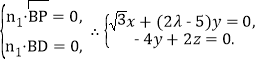

取y=,得z=2,x=5-2λ,

故n1=(5-2λ,,2).

又平面ABP的法向量为n2=(0,0,1),

因此cos<n1,n2>=,解得λ=1或λ=4.

故=4