题目内容
【题目】已知空间中三点A(-2,0,2),B(-1,1,2),C(-3,0,4),设a=![]() ,b=
,b=![]() .
.
(1)求向量a与向量b的夹角的余弦值;
(2)若ka+b与ka-2b互相垂直,求实数k的值
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
试题分析:(1)第一步,求出两个向量的坐标,第二步,分别计算![]() ,和
,和![]() ,最后代入公式
,最后代入公式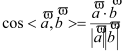 ;
;
(2)方法一,先得到![]() 和
和![]() 的坐标,然后代入数量积的坐标表示,可得
的坐标,然后代入数量积的坐标表示,可得![]() 的值;
的值;
方法二,先计算(![]() )(
)(![]() )
)![]() ,然后代入两个向量的坐标表示,求
,然后代入两个向量的坐标表示,求![]() 的值.
的值.
试题解析:解 (1)∵a=(1,1,0),b=(-1,0,2), ∴a·b=(1,1,0)·(-1,0,2)=-1,
又|a|=![]() =
=![]() , |b|=
, |b|=![]() =
=![]() ,
,
∴cos〈a,b〉=![]() =
=![]() =-
=-![]() , 即向量a与向量b的夹角的余弦值为-
, 即向量a与向量b的夹角的余弦值为-![]() .
.
(2)方法一 ∵ka+b=(k-1,k,2).ka-2b=(k+2,k,-4),且ka+b与ka-2b互相垂直,
∴(k-1,k,2)·(k+2,k,-4)=(k-1)(k+2)+k2-8=0, ∴k=2或k=-![]() ,
,
∴当ka+b与ka-2b互相垂直时,实数k的值为2或-![]() .、
.、
方法二 由(1)知|a|=![]() ,|b|=
,|b|=![]() ,a·b=-1,
,a·b=-1,
∴(ka+b)·(ka-2b)=k2a2-ka·b-2b2=2k2+k-10=0, 得k=2或k=-![]() .
.

练习册系列答案
相关题目