题目内容
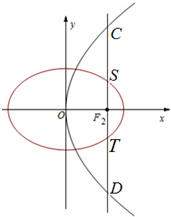
如图,椭圆C1:
+
=1(a>b>0)和圆C2:x2+y2=b2,已知圆C2将椭圆C1的长轴三等分,椭圆C1右焦点到右准线的距离为
,椭圆C1的下顶点为E,过坐标原点O且与坐标轴不重合的任意直线l与圆C2相交于点A、B.
(1)求椭圆C1的方程;
(2)若直线EA、EB分别与椭圆C1相交于另一个交点为点P、M.
①求证:直线MP经过一定点;
②试问:是否存在以(m,0)为圆心,
为半径的圆G,使得直线PM和直线AB都与圆G相交?若存在,请求出所有m的值;若不存在,请说明理由.

| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 4 |
(1)求椭圆C1的方程;
(2)若直线EA、EB分别与椭圆C1相交于另一个交点为点P、M.
①求证:直线MP经过一定点;
②试问:是否存在以(m,0)为圆心,
3
| ||
| 5 |

(1)由圆C2将椭圆C1的长轴三等分,∴2b=
•2a,则a=3b.
∴c=
=2
b,
又椭圆C1右焦点到右准线的距离为
,
∴
-c=
=
,∴b=1,则a=3,
∴椭圆方程为
+y2=1.
(2)①由题意知直线PE,ME的斜率存在且不为0,设直线PE的斜率为k,则PE:y=kx-1,
由
得
或
∴P(
,
),
用-
去代k,得M(
,
),
kPM=
=
,
∴PM:y-
=
(x+
),即y=
x+
,
∴直线PM经过定点T(0,
).
②由
得
或
∴A(
,
),
则直线AB:y=
x,
设t=
,则t∈R,直线PM:y=tx+
,直线AB:y=5tx,
假设存在圆心为(m,0),半径为
的圆G,使得直线PM和直线AB都与圆G相交,
则(i)
<
,(ii)
<
.
由(i)得25t2(m2-
)<
对t∈R恒成立,则m2≤
,
由(ii)得,(m2-
)t2+
mt-
<0对t∈R恒成立,
当m2=
时,不合题意;当m2<
时,△=(
m)2-4(m2-
)(-
)<0,得m2<
,即-
<m<
,
∴存在圆心为(m,0),半径为
的圆G,使得直线PM和直线AB都与圆G相交,所有m的取值集合为(-
,
).
| 1 |
| 3 |
∴c=
| a2-b2 |
| 2 |
又椭圆C1右焦点到右准线的距离为
| ||
| 4 |
∴
| a2 |
| c |
| b2 |
| c |
| ||
| 4 |
∴椭圆方程为
| x2 |
| 9 |
(2)①由题意知直线PE,ME的斜率存在且不为0,设直线PE的斜率为k,则PE:y=kx-1,
由
|
|
|
∴P(
| 18k |
| 9k2+1 |
| 9k2-1 |
| 9k2+1 |
用-
| 1 |
| k |
| -18k |
| k2+9 |
| 9-k2 |
| k2+9 |
kPM=
| ||||
|
| k2-1 |
| 10k |
∴PM:y-
| 9-k2 |
| k2+9 |
| k2-1 |
| 10k |
| 18k |
| k2+9 |
| k2-1 |
| 10k |
| 4 |
| 5 |
∴直线PM经过定点T(0,
| 4 |
| 5 |
②由
|
|
|
∴A(
| 2k |
| 1+k2 |
| k2-1 |
| k2+1 |
则直线AB:y=
| k2-1 |
| 2k |
设t=
| k2-1 |
| 10k |
| 4 |
| 5 |
假设存在圆心为(m,0),半径为
3
| ||
| 5 |
则(i)
| |5tm| | ||
|
3
| ||
| 5 |
|tm+
| ||
|
3
| ||
| 5 |
由(i)得25t2(m2-
| 18 |
| 25 |
| 18 |
| 25 |
| 18 |
| 25 |
由(ii)得,(m2-
| 18 |
| 25 |
| 8 |
| 5 |
| 2 |
| 25 |
当m2=
| 18 |
| 25 |
| 18 |
| 25 |
| 8 |
| 5 |
| 18 |
| 25 |
| 2 |
| 25 |
| 2 |
| 25 |
| ||
| 5 |
| ||
| 5 |
∴存在圆心为(m,0),半径为
3
| ||
| 5 |
| ||
| 5 |
| ||
| 5 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目