题目内容
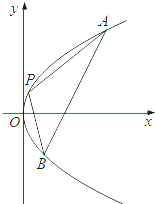
点P（4，4），圆C：（x-1）2+y2=5与椭圆E：
+
=1有一个公共点A（3，1），F1、F2分别是椭圆左、右焦点，直线PF1与圆C相切．设Q为椭圆E上的一个动点，求
•
的取值范围．
| x2 |
| 18 |
| y2 |
| 2 |
| AP |
| AQ |
∵A（3，1），P（4，4），
∴
=(1，3)，
设Q（x，y），则
=(x-3，y-1)，
∴
•
=(x-3)+3(y-1)=x+3y-6．
∵
+
=1，
即x2+（3y）2=18，而x2+（3y）2≥2|x|•|3y|，
∴-18≤6xy≤18．则（x+3y）2=x2+（3y）2+6xy=18+6xy的取值范围是[0，36]．
∴x+3y的取值范围是[-6，6]，
因此，
•
的取值范围是[-12，0]．
∴
| AP |
设Q（x，y），则
| AQ |
∴
| AP |
| AQ |
∵
| x2 |
| 18 |
| y2 |
| 2 |
即x2+（3y）2=18，而x2+（3y）2≥2|x|•|3y|，
∴-18≤6xy≤18．则（x+3y）2=x2+（3y）2+6xy=18+6xy的取值范围是[0，36]．
∴x+3y的取值范围是[-6，6]，
因此，
| AP |
| AQ |
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
