题目内容
p:?x0∈R,使得ax02-2x0-1>0成立;q:方程x2+(a-3)x+a=0有两个不相等正实根;
(1)写出¬p;
(2)若命题¬p为真命题,求实数a的取值范围;
(3)若命题“p或q”为真命题,且“p且q”为假命题,求实数a的取值范围.
(1)写出¬p;
(2)若命题¬p为真命题,求实数a的取值范围;
(3)若命题“p或q”为真命题,且“p且q”为假命题,求实数a的取值范围.
(1)p:?x0∈R,使得ax02-2x0-1>0成立;∴¬p?x∈R,ax2-2x-1≤0成立.
(2)a≥0时ax2-2x-1≤0不恒成立.
由
,即
,解得a≤-1.
∴实数a的取值范围:(-∞,-1].
(3)设方程x2+(a-3)x+a=0两个不相等正实根为x1、x2.
命题q为真?
?
解得0<a<1.
由命题“p或q”为真,且“p且q”为假,得命题p、q一真一假
①当p真q假时,则
得-1<a≤0或a≥1
②当p假q真时,则
无解;
∴实数a的取值范围是-1<a≤0或a≥1.
(2)a≥0时ax2-2x-1≤0不恒成立.
由
|
|
∴实数a的取值范围:(-∞,-1].
(3)设方程x2+(a-3)x+a=0两个不相等正实根为x1、x2.
命题q为真?
|
|
由命题“p或q”为真,且“p且q”为假,得命题p、q一真一假
①当p真q假时,则
|
②当p假q真时,则
|
∴实数a的取值范围是-1<a≤0或a≥1.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在
在 上是增函数.
上是增函数. 的取值范围
的取值范围 ;
;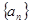 满足:
满足: ,且
,且 ,
, ,并判断
,并判断 与
与 的大小.
的大小.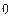 。
。