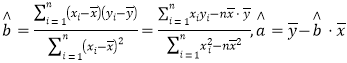ЬтФПФкШн
ЁОЬтФПЁПОЙлВтЃЌФГРЅГцЕФВњТбЪ§yгыЮТЖШxгаЙиЃЌЯжНЋЪеМЏЕНЕФЮТЖШxiКЭВњТбЪ§yiЃЈi=1ЃЌ2ЃЌЁЃЌ10ЃЉЕФ10зщЙлВтЪ§ОнзїСЫГѕВНДІРэЃЌЕУЕНШчЯТЭМЕФЩЂЕуЭММАвЛаЉЭГМЦСПБэЃЎ
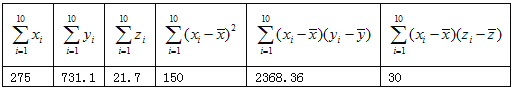
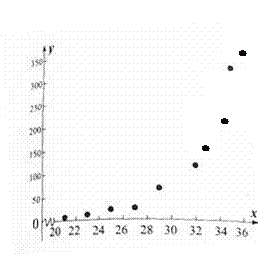
Бэжа![]() ,
, ![]()
ЃЈ1ЃЉИљОнЩЂЕуЭМХаЖЯЃЌ ![]() ,
, ![]() гы
гы![]() ФФвЛИіЪЪвЫзїЮЊyгыxжЎМфЕФЛиЙщЗНГЬФЃаЭЃПЃЈИјГіХаЖЯМДПЩЃЌВЛБиЫЕУїРэгЩЃЉ
ФФвЛИіЪЪвЫзїЮЊyгыxжЎМфЕФЛиЙщЗНГЬФЃаЭЃПЃЈИјГіХаЖЯМДПЩЃЌВЛБиЫЕУїРэгЩЃЉ
ЃЈ2ЃЉИљОнЃЈ1ЃЉЕФХаЖЯНсЙћМАБэжаЪ§ОнЃЎ
ЂйЪдЧѓyЙигкxЛиЙщЗНГЬЃЛ
ЂквбжЊгУШЫЙЄХрбјИУРЅГцЕФГЩБОhЃЈxЃЉгыЮТЖШxКЭВњТбЪ§yЕФЙиЯЕЮЊhЃЈxЃЉ=xЃЈlnyЉ2.4ЃЉ+170ЃЌЕБЮТЖШxЃЈxШЁећЪ§ЃЉЮЊКЮжЕЪБЃЌХрбјГЩБОЕФдЄБЈжЕзюаЁЃП
ИНЃКЖдгквЛзщЪ§ОнЃЈu1ЃЌv1ЃЉЃЌЃЈu2ЃЌv2ЃЉЃЌЁЃЈunЃЌvnЃЉЃЌЦфЛиЙщжБЯпv=ІС+ІТuЕФаБТЪКЭНиОрЕФзюаЁЖўГЫЙРМЦЗжБ№ЮЊІТ=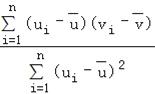 ЃЌІС=
ЃЌІС=![]() ЉІТ
ЉІТ![]() ЃЎ
ЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉМћНтЮі.
ЃЛЃЈ2ЃЉМћНтЮі.
ЁОНтЮіЁПЗжЮіЃКЃЈ1ЃЉИљОнЩЂЕуЭМХаЖЯЃЌПДГібљБОЕуЗжВМдквЛЬѕжИЪ§КЏЪ§ЕФжмЮЇЃЌПЩЕУНсТлЃЛ
ЃЈ2ЃЉЂйгЩБфЛЛКѓЕФбљБОЕуЗжВМдквЛЬѕжБЯпИННќЃЌвђДЫПЩвдгУЯпадЛиЙщЗНГЬРДФтКЯЃЌМДПЩЧѓГіyЖдxЕФЛиЙщЗНГЬЃЛ
ЂкДњШызЊЛЏЮЊЖўДЮКЏЪ§ЕФзюжЕЮЪЬтЃЌНсКЯЖўДЮКЏЪ§ЕФЭМЯѓгыаджЪПЩЕУНсТлЃЎ
ЯъНтЃКЃЈ1ЃЉИљОнЩЂЕуЭМХаЖЯЃЌПДГібљБОЕуЗжВМдквЛЬѕжИЪ§КЏЪ§ЕФжмЮЇЃЌЫљвд![]() ЪЪвЫзїЮЊyгыxжЎМфЕФЛиЙщЗНГЬФЃаЭЃЛ
ЪЪвЫзїЮЊyгыxжЎМфЕФЛиЙщЗНГЬФЃаЭЃЛ
ЃЈ2ЃЉЂй Сюz=lny ЃЌ ![]()
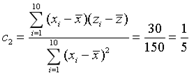
![]()
![]()
![]()
Ђк![]()
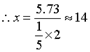 ЪБЃЌХрбјГЩБОЕФдЄБЈжЕзюаЁЃЎ
ЪБЃЌХрбјГЩБОЕФдЄБЈжЕзюаЁЃЎ

ЁОЬтФПЁПЮЊСЫНтбЇЩњЕФПЮЭтдФЖСЪБМфЧщПіЃЌФГбЇаЃЫцЛњГщШЁСЫ50ШЫНјааЭГМЦЗжЮіЃЌАбет50ШЫУПЬьдФЖСЕФЪБМфЃЈЕЅЮЛЃКЗжжгЃЉЛцжЦГЩЦЕЪ§ЗжВМБэЃЌШчЯТБэЫљЪОЃК
дФЖСЪБМф | [0,20ЃЉ | [20,40ЃЉ | [40,60ЃЉ | [60,80ЃЉ | [80,100ЃЉ | [100,120] |
ШЫЪ§ | 8 | 10 | 12 | 11 | 7 | 2 |
ШєАбУПЬьдФЖСЪБМфдк60ЗжжгвдЩЯЃЈКЌ60ЗжжгЃЉЕФЭЌбЇГЦЮЊЁАдФЖСДяШЫЁБЃЌИљОнЭГМЦНсЙћжаФаХЎЩњдФЖСДяШЫЕФЪ§ОнЃЌжЦзїГіШчЭМЫљЪОЕФЕШИпЬѕаЮЭМЃК

ЃЈ1ЃЉИљОнвбжЊЬѕМўЭъГЩ2x2СаСЊБэ;
ФаЩњ | ХЎЩњ | змМЦ | |
дФЖСДяШЫ | |||
ЗЧдФЖСДяШЫ | |||
змМЦ |
ЃЈ2ЃЉВЂХаЖЯЪЧЗёга![]() ЕФАбЮеШЯЮЊЁАдФЖСДяШЫЁБИњадБ№гаЙиЃП
ЕФАбЮеШЯЮЊЁАдФЖСДяШЫЁБИњадБ№гаЙиЃП
ИНЃКВЮПМЙЋЪН![]()
![]()
ЁОЬтФПЁПЧнСїИавЛжБдкЭўаВЮвУЧЕФЩњЛюЃЌФГМВВЁПижЦжааФЮЊСЫбаОПЧнСїИаВЁЖОЗБжГИіЪ§![]() ЃЈИіЃЉЫцЪБМф
ЃЈИіЃЉЫцЪБМф![]() ЃЈЬьЃЉБфЛЏЕФЙцТЩЃЌЪеМЏЪ§ОнШчЯТЃК
ЃЈЬьЃЉБфЛЏЕФЙцТЩЃЌЪеМЏЪ§ОнШчЯТЃК
ЬьЪ§ | 1 | 2 | 3 | 4 | 5 | 6 |
ЗБжГИіЪ§ | 6 | 12 | 25 | 49 | 95 | 190 |
зїГіЩЂЕуЭМПЩПДГібљБОЕуЗжВМдквЛЬѕжИЪ§аЭКЏЪ§![]() ЕФжмЮЇ.
ЕФжмЮЇ.
БЃСєаЁЪ§ЕуКѓСНЮЛЪ§ЕФВЮПМЪ§ОнЃК
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЦфжа
ЃЌЦфжа![]()
ЃЈ1ЃЉЧѓГі![]() Йигк
Йигк![]() ЕФЛиЙщЗНГЬЃЈБЃСєаЁЪ§ЕуКѓСНЮЛЪ§зжЃЉЃЛ
ЕФЛиЙщЗНГЬЃЈБЃСєаЁЪ§ЕуКѓСНЮЛЪ§зжЃЉЃЛ
ЃЈ2ЃЉвбжЊ![]() ЃЌЙРЫуЕкЫФЬьЕФВаВю.
ЃЌЙРЫуЕкЫФЬьЕФВаВю.
ВЮПМЙЋЪНЃК