题目内容
【题目】选修4—4：坐标系与参数方程
在直线坐标系xoy中，圆C的方程为（x+6）2+y2=25.
（1）以坐标原点为极点，x轴正半轴为极轴建立极坐标系，求C的极坐标方程；
（2）直线l的参数方程是 
（t为参数）,l与C交于A、B两点，∣AB∣= 
，求l的斜率。
【答案】
（1）
解：整理圆的方程得 
，
由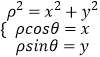 
可知圆 
的极坐标方程为 
（2）
解：记直线的斜率为 
，则直线的方程为 
，
由垂径定理及点到直线距离公式知： 
，
即 
，整理得 
，则 
【解析】（1）把圆C的标准方程化为一般方程，由此利用ρ2=x2+y2 ， x=ρcosα，y=ρsinα，能求出圆C的极坐标方程．（2）由直线l的参数方程求出直线l的一般方程，再求出圆心到直线距离，由此能求出直线l的斜率．
【考点精析】认真审题，首先需要了解圆的标准方程(圆的标准方程：
；圆心为A(a,b),半径为r的圆的方程)．
练习册系列答案
相关题目
