Question

【题目】函数f(x)=Asin(ωx+φ)的部分图象如图所示.

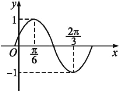
(1)求f(x)的最小正周期及解析式;

(2)设函数g(x)=f(x)-cos 2x,求g(x)在区间上的最小值.

Answer 1

【答案】（1）T=π,f(x)=sin；（2）.

【解析】

由图象可得，，从而可求，再由图象经过点可以求得，代入即可写出函数的解析式

求出，以为整体求值即可

(1)由图可得A=1,,所以T=π,因此ω=2.

当x=时,由f(x)=1,可得sin=1,即+φ=kπ+,k∈Z,又|φ|<,所以φ=,

故f(x)=sin.

(2)由(1)知g(x)=f(x)-cos 2x=sin-cos 2x=sin 2x+cos 2x-cos 2x=sin 2x-cos 2x=sin,

因为x∈,所以-≤2x-,

故当2x-=-,即x=0时,函数g(x)取最小值.