题目内容
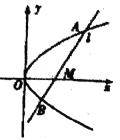
【题目】已知抛物线![]() =
=![]() 的焦点
的焦点![]() 为坐标原点,
为坐标原点, ![]() 是抛物线
是抛物线![]() 上异于
上异于![]() 的两点.
的两点.
(1)求抛物线![]() 的方程;
的方程;
(2)若直线![]() 的斜率之积为
的斜率之积为![]() ,求证:直线
,求证:直线![]() 过
过![]() 轴上一定点.
轴上一定点.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:本题主要考查抛物线方程、直线与圆锥曲线的位置关系、直线的方程与斜率,考查了定点问题.(1)由抛物线的焦点坐标可得p的值,即可得抛物线方程;(2)分直线的斜率存在与不存在两种情况,结合直线![]() 的斜率之积为
的斜率之积为![]() 进行讨论.
进行讨论.
试题解析:
(1)因为抛物线![]() 的焦点坐标为
的焦点坐标为![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以抛物线![]() 的方程为
的方程为![]() .
.
(2)证明:①当直线![]() 的斜率不存在时,
的斜率不存在时,
设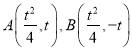 .
.
因为直线![]() 的斜率之积为
的斜率之积为![]() ,
,
所以![]() =
=![]() ,化简得
,化简得![]() ,
,
所以![]() ,此时直线
,此时直线![]() 的方程为
的方程为![]() .
.
②当直线![]() 的斜率存在时,
的斜率存在时,
设其方程为![]() =
= ![]() ,
,
联立方程组![]() 消去
消去![]() ,
,
得![]() ,
,
根据根与系数的关系得![]() ,因为直线
,因为直线![]() 的斜率之积为
的斜率之积为![]() ,
,
所以![]() =
=![]() ,即
,即![]() ,即
,即![]() ,
,
解得![]() (舍去)或
(舍去)或![]() ,
,
所以![]() =
=![]() =
=![]() ,即
,即![]() ,
,
所以![]() ,即
,即![]() ,
,
综上所述,直线![]() 过定点
过定点![]() .
.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目