题目内容
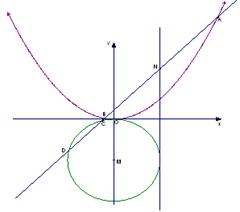
已知定点F(1,0),动点P在y轴上运动,过点P作PM交x轴于点M,并延长MP到点N,且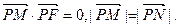
(Ⅰ)求动点N的轨迹方程;
(Ⅱ)直线l与动点N的轨迹交于A、B两点,若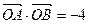 ,且
,且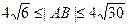 ,
,
求直线l的斜率k的取值范围.
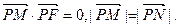
(Ⅰ)求动点N的轨迹方程;
(Ⅱ)直线l与动点N的轨迹交于A、B两点,若
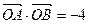 ,且
,且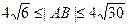 ,
,求直线l的斜率k的取值范围.
(Ⅰ)设N(x,y),P(0,y0) |PM|=|PN|
∴P为MN的中点,∴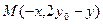 ………………(1分)
………………(1分)
M在x轴上, ∴2y0-y="0 " 即为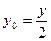 ∴
∴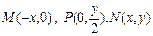
∴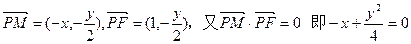 ∴y2="4x "
∴y2="4x "
故点N的轨迹方程为y2="4x " ………………(5分)
(Ⅱ)F(1,0)恰为y2=4x的焦点,设l为: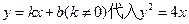
得: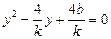 设
设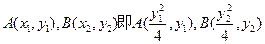
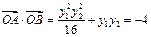 ∴
∴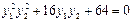
∴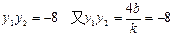 ∴b=-2k ………………(9分)
∴b=-2k ………………(9分)
即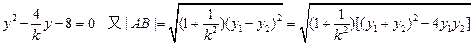
∴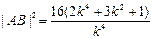 ∴16×6
∴16×6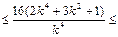 16×30 解得
16×30 解得 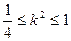
∴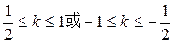 …………(13分)
…………(13分)
∴P为MN的中点,∴
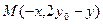 ………………(1分)
………………(1分)M在x轴上, ∴2y0-y="0 " 即为
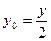 ∴
∴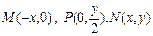
∴
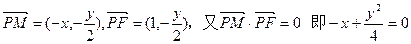 ∴y2="4x "
∴y2="4x " 故点N的轨迹方程为y2="4x " ………………(5分)
(Ⅱ)F(1,0)恰为y2=4x的焦点,设l为:
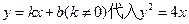
得:
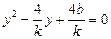 设
设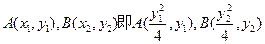
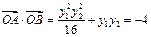 ∴
∴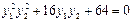
∴
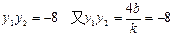 ∴b=-2k ………………(9分)
∴b=-2k ………………(9分)即
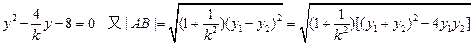
∴
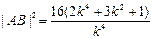 ∴16×6
∴16×6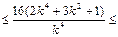 16×30 解得
16×30 解得 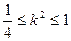
∴
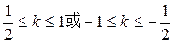 …………(13分)
…………(13分)略

练习册系列答案
相关题目
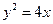 ,F是焦点,直线l是经过点F的任意直线.
,F是焦点,直线l是经过点F的任意直线.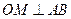 (O是坐标原点,M是垂足),求动点M的轨迹方程;
(O是坐标原点,M是垂足),求动点M的轨迹方程;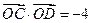 ,求证直线CD必过定点,并求出定点的坐标.
,求证直线CD必过定点,并求出定点的坐标.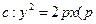 >0)上有两动点A、B(AB不垂直
>0)上有两动点A、B(AB不垂直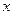 轴),F为焦点,且
轴),F为焦点,且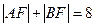 ,又线段AB的垂直平分线经过定点Q(6,0),求抛物线方程。
,又线段AB的垂直平分线经过定点Q(6,0),求抛物线方程。
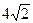
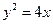 上一点
上一点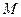 到焦点的距离为3,则点
到焦点的距离为3,则点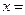 .
.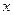 轴上的抛物线截直线
轴上的抛物线截直线 所得的弦长|AB|=
所得的弦长|AB|=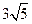 ,求此抛物线的方程。
,求此抛物线的方程。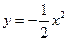 的焦点坐标是___ ,
的焦点坐标是___ ,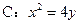 ,圆
,圆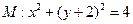 ,
,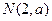 (其中
(其中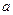 为常数)是
为常数)是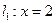 上的点,倾斜角为锐角
上的点,倾斜角为锐角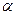 的直线
的直线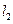 过点
过点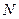 且与抛物线C交于两点A、B,与圆M交于C、D两点.
且与抛物线C交于两点A、B,与圆M交于C、D两点.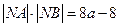 ,且
,且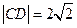 ,求
,求