题目内容
(本题满分12分)本题共有2个小题,第1小题满分5分,第2小题满分7分.
已知抛物线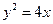 ,F是焦点,直线l是经过点F的任意直线.
,F是焦点,直线l是经过点F的任意直线.
(1)若直线l与抛物线交于两点A、B,且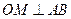 (O是坐标原点,M是垂足),求动点M的轨迹方程;
(O是坐标原点,M是垂足),求动点M的轨迹方程;
(2)若C、D两点在抛物线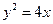 上,且满足
上,且满足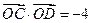 ,求证直线CD必过定点,并求出定点的坐标.
,求证直线CD必过定点,并求出定点的坐标.
已知抛物线
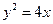 ,F是焦点,直线l是经过点F的任意直线.
,F是焦点,直线l是经过点F的任意直线.(1)若直线l与抛物线交于两点A、B,且
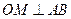 (O是坐标原点,M是垂足),求动点M的轨迹方程;
(O是坐标原点,M是垂足),求动点M的轨迹方程;(2)若C、D两点在抛物线
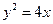 上,且满足
上,且满足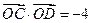 ,求证直线CD必过定点,并求出定点的坐标.
,求证直线CD必过定点,并求出定点的坐标.所求动点M的轨迹方程是 (
(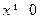 ).
).
直线CD的方程可化为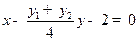 . 直线CD恒过定点,且定点坐标为(2,0).
. 直线CD恒过定点,且定点坐标为(2,0).
 (
(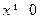 ).
).直线CD的方程可化为
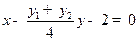 . 直线CD恒过定点,且定点坐标为(2,0).
. 直线CD恒过定点,且定点坐标为(2,0).(本题满分12分)本题共有2个小题,第1小题满分5分,第2小题满分7分.
解 (1) 设动点M的坐标为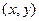 . …………………1分
. …………………1分
∵抛物线 的焦点是
的焦点是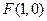 ,直线l恒过点F,且与抛物线交于两点A、B,
,直线l恒过点F,且与抛物线交于两点A、B,
又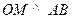 ,
,
∴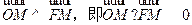 . …………………3分
. …………………3分
∴ ,化简,得
,化简,得 . …………………5分
. …………………5分
又当M与原点重合时,直线l与x轴重合,故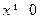 .
.
∴所求动点M的轨迹方程是 (
(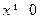 ).
).
(2) 设点C、D的坐标为 、
、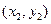 . …………………………6分
. …………………………6分
∵C、D在抛物线 上,
上,
∴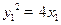 ,
,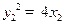 ,即
,即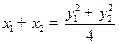 ,
,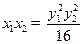 .
.
又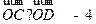 ,
,
∴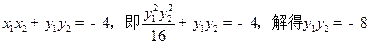 . ………8分
. ………8分
∵点C、D的坐标为 、
、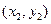 ,
,
∴直线CD的一个法向量是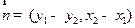 ,可得直线CD的方程为:
,可得直线CD的方程为:
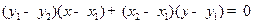 ,化简,得
,化简,得
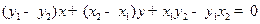 ,进一步用
,进一步用 ,有
,有
 .
.
又抛物线 上任两点的纵坐标都不相等,即
上任两点的纵坐标都不相等,即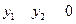 .
.
∴直线CD的方程可化为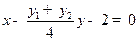 . ………………………10分
. ………………………10分
∴直线CD恒过定点,且定点坐标为(2,0). ………………………12分
解 (1) 设动点M的坐标为
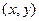 . …………………1分
. …………………1分∵抛物线
 的焦点是
的焦点是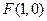 ,直线l恒过点F,且与抛物线交于两点A、B,
,直线l恒过点F,且与抛物线交于两点A、B,又
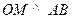 ,
,∴
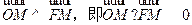 . …………………3分
. …………………3分∴
 ,化简,得
,化简,得 . …………………5分
. …………………5分又当M与原点重合时,直线l与x轴重合,故
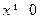 .
.∴所求动点M的轨迹方程是
 (
(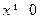 ).
).(2) 设点C、D的坐标为
 、
、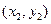 . …………………………6分
. …………………………6分∵C、D在抛物线
 上,
上,∴
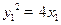 ,
,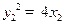 ,即
,即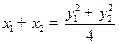 ,
,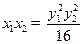 .
.又
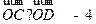 ,
,∴
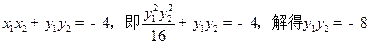 . ………8分
. ………8分∵点C、D的坐标为
 、
、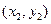 ,
,∴直线CD的一个法向量是
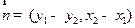 ,可得直线CD的方程为:
,可得直线CD的方程为: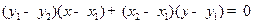 ,化简,得
,化简,得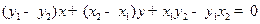 ,进一步用
,进一步用 ,有
,有 .
.又抛物线
 上任两点的纵坐标都不相等,即
上任两点的纵坐标都不相等,即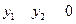 .
.∴直线CD的方程可化为
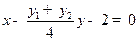 . ………………………10分
. ………………………10分∴直线CD恒过定点,且定点坐标为(2,0). ………………………12分

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
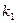 ,直线OB的斜率为
,直线OB的斜率为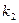 .
.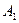 、
、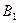 ,求
,求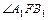 的大小.
的大小.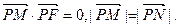
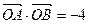 ,且
,且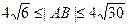 ,
,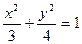 的焦点F与抛物线C:
的焦点F与抛物线C: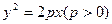 的焦点关于直线x-y=0
的焦点关于直线x-y=0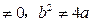 ),M是抛物线C上的点,设直线AM,
),M是抛物线C上的点,设直线AM,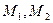 .求证:当M点在抛物线上变动时(只要
.求证:当M点在抛物线上变动时(只要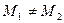 )直线
)直线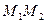 恒过一定点,并求出这个定点的坐标.
恒过一定点,并求出这个定点的坐标.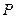 为抛物线
为抛物线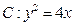 上的一个动点,
上的一个动点,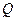 为圆
为圆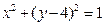 上的动点,设点
上的动点,设点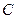 的准线距离为
的准线距离为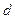 ,则
,则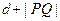 的最小值为
的最小值为 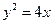 的焦点
的焦点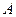 的直线交该抛物线于
的直线交该抛物线于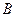 两点,
两点,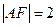 ,则
,则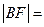 ___________ .
___________ .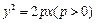 的焦点为
的焦点为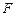 ,点
,点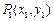 、
、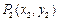 、
、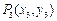 在抛物线上,且
在抛物线上,且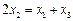 ,则有
,则有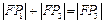
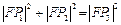
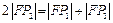
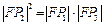
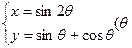 为参数)表示的曲线是( )
为参数)表示的曲线是( )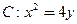 上一点P到定点A(0,1)的距离为2,则点P到
上一点P到定点A(0,1)的距离为2,则点P到