��Ŀ����
15����֪��Բ$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1����ֱ��l1��ԭ�㣬ֱ��l2��ֱ��l1�ཻ�ڵ�P��ح$\overrightarrow{OP}$ح=1����l1��l2��ֱ��l2����Բ����A��B���㣬���Ƿ����������ֱ��l2��ʹ$\overrightarrow{AP•}\overrightarrow{PB}$=1�����������ڣ����ֱ��l2�ķ��̣��������ڣ���˵�����ɣ����� �������ۣ�����$\overrightarrow{AP•}\overrightarrow{PB}$=1��ح$\overrightarrow{OP}$ح=1����ת������ֱ��l2�ķ���Ϊmx+ny=1������Բ���̣�����x1x2+y1y2=0�����ɵó����ۣ�
��� �⣺�������ֱ��l2��ʹ$\overrightarrow{AP•}\overrightarrow{PB}$=1������
��A��B���������ֱ�Ϊ��x1��y1������x2��y2����Q��m��n������m2+n2=1��
��ֱ��l1�ķ���Ϊnx-my=0��ֱ��l2�ķ���Ϊmx+ny=1��
��1����n=0ʱ����ʱֱ��l2�ķ���Ϊx=��1���ɵ�A��1��$\frac{\sqrt{14}}{2}$����B��1��-$\frac{\sqrt{14}}{2}$����
����$\overrightarrow{AP•}\overrightarrow{PB}$��1���������⣻ ����5�֣�
��2����n��0ʱ����ֱ��l2�ķ���Ϊmx+ny=1����Բ����$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1������
��m2+n2=1���� ��1+m2��x2-4mx+2-8n2=0������6�֣�
��x1+x2=$\frac{4m}{1+{m}^{2}}$��x1x2=$\frac{2-8{n}^{2}}{1+{m}^{2}}$�� ����7�֣�
�֡�$\overrightarrow{AP•}\overrightarrow{PB}$=1��
��x1x2+y1y2+2=m��x1+x2��+n��y1+y2����
�� mx1+ny1=1��mx2+ny2=1
��m��x1+x2��+n��y1+y2��=2��
��x1x2+y1y2=0�� ����9�֣�
��n2x1x2+1+m2x1x2-m��x1+x2��=0��
��x1x2+1-m��x1+x2��=0�� ����11�֣�
��-5n2=0��
��n=0����n��0ì�ܣ� ����12�֣�
���Ͽ�֪��������������ֱ��l2��ʹ$\overrightarrow{AP•}\overrightarrow{PB}$=1������
���� ���⿼����Բ���̣�����ֱ������Բ��λ�ù�ϵ������������۵���ѧ˼�룬����ѧ�������������������������е��⣮

 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д�| A�� | ��0��$\frac{1}{4}$] | B�� | [-1��$\frac{1}{4}$] | C�� | ��0��$\frac{1}{8}$] | D�� | [-1��$\frac{1}{8}$] |
| ҽ�ƶ�\�Ա� | ��ҽ�� | Ůҽʦ |
| �� | 6 | 4 |
| �� | 3 | 2 |
��2����X��ʾ��ȡ����ҽ������������X�ķֲ��м���ѧ������
| A�� | $\frac{��}{16}$ | B�� | $\frac{��}{8}$ | C�� | $\frac{��}{4}$ | D�� | $\frac{��}{2}$ |
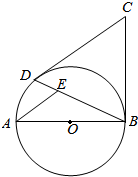 ��ͼ������CD��CB�ֱ����O�ཻ�ڵ�D��B��ABΪ��O��ֱ����AE��CD��BD�ڵ�E����AB=BC����sin��BAE��ֵΪ$\frac{3}{5}$��
��ͼ������CD��CB�ֱ����O�ཻ�ڵ�D��B��ABΪ��O��ֱ����AE��CD��BD�ڵ�E����AB=BC����sin��BAE��ֵΪ$\frac{3}{5}$��