题目内容
3.求函数y=arcsin(sinx)的定义域、值域、判断它的奇偶性、单调性、周期性.分析 由条件利用反正弦函数的定义和性质,求得函数y=arcsin(sinx)的定义域、值域、判断它的奇偶性、单调性、周期性.
解答 解:对于函数y=arcsin(sinx),根据-1≤sinx≤1,求得x∈R,故函数的定义域为R.
根据反正弦函数的定义可得y∈[-$\frac{π}{2}$,$\frac{π}{2}$].
再根据y=f(x)=arcsin(sinx)满足f(-x)=arcsin[sin(-x)]=arcsin[-sinx]=-arcsin(sinx)=-f(x),
故函数f(x)为奇函数.
在R上,当x增大时,函数t=sinx没有单调性,故函数y=arcsin(sinx)没有单调性.
再根据y=f(x)=arcsin(sinx)满足f(x+2π)=arcsin[sin(x+2π)]=arcsin(sinx)=f(x),
可得函数y的一个周期为2π.
由于不存在T∈(0,2π),使f(x+T)=f(x)对于定义域内的任意x都成立,故函数y的周期为2π.
点评 本题主要考查反正弦函数的定义和性质,属于中档题.

练习册系列答案
相关题目
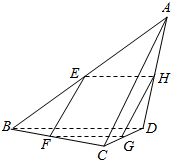 如图,空间四边形ABCD中,AC、BD成60°角,且AC=4,BD=2$\sqrt{3}$,四个点E、F、G、H分别是边AB、BC、CD、DA的中点,求SEFGH.
如图,空间四边形ABCD中,AC、BD成60°角,且AC=4,BD=2$\sqrt{3}$,四个点E、F、G、H分别是边AB、BC、CD、DA的中点,求SEFGH.