题目内容
4.若函数f(x)=e2x+1-ax+1,a∈R.(1)f(x)的单调递增区间;
(2)若f(x)≥1,对任意x∈[0,1]都成立,求实数a的取值范围.
分析 (1)先求导数,对参数a分类讨论,分别令导数大于零,小于零,解出x的范围即可;
(2)若f(x)≥1,对任意x∈[0,1]都成立,则函数f(x)的最小值不小于1,利用导数法,求出函数的最值,可得答案.
解答 解:(1)∵f(x)=e2x+1-ax+1,
∴f′(x)=2e2x+1-a,
当a≤0时,f′(x)>0恒成立,所以f(x)在(-∞,+∞)上为增函数;…(2分)
当a>0时,由f′(x)=0得x=ln$\sqrt{\frac{a}{2e}}$,且当x∈(-∞,ln$\sqrt{\frac{a}{2e}}$)时,f′(x)<0,
当x∈(ln$\sqrt{\frac{a}{2e}}$,+∞)时f′(x)>0,
所以f(x)在x∈(-∞,ln $\sqrt{\frac{a}{2e}}$)为减函数,在x∈(ln$\sqrt{\frac{a}{2e}}$,+∞)为增函数.…(4分)
(2)由(1)知,
当a≤0时,函数f(x)在区间[0,1]上为增函数,此时当x=0时,函数取最小值e+1,
满足f(x)≥1恒成立,
当0<a<2e3时,ln$\sqrt{\frac{a}{2e}}$<1,函数f(x)在区间[0,ln$\sqrt{\frac{a}{2e}}$]上为减函数,在区间[ln$\sqrt{\frac{a}{2e}}$,1]上为增函数,
此时当x=ln$\sqrt{\frac{a}{2e}}$时,函数函数f(x)取最小值$\frac{a}{2}-a•ln\sqrt{\frac{a}{2e}}$+1,
若f(x)≥1,则$\frac{a}{2}-a•ln\sqrt{\frac{a}{2e}}$+1≥1,即$\frac{a}{2}-a•ln\sqrt{\frac{a}{2e}}$≥0,
解得:0<a≤2e2,
当a≥2e3时,ln$\sqrt{\frac{a}{2e}}$≥1,函数f(x)在区间[0,1]上为减函数,此时当x=1时,函数取最小值e3-a+1,
若f(x)≥1,则e3-a+1≥1,即a≤e3,
∴此时不存在满足条件的a值,
综上所述实数a的取值范围为(-∞,2e2]
点评 本题考查导数的综合应用,属于中档题,要求考生会利用导数研究函数的单调区间以及根据函数的增减性得到函数的最值.掌握不等式恒成立时所取的条件.

 阅读快车系列答案
阅读快车系列答案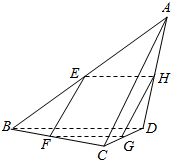 如图,空间四边形ABCD中,AC、BD成60°角,且AC=4,BD=2$\sqrt{3}$,四个点E、F、G、H分别是边AB、BC、CD、DA的中点,求SEFGH.
如图,空间四边形ABCD中,AC、BD成60°角,且AC=4,BD=2$\sqrt{3}$,四个点E、F、G、H分别是边AB、BC、CD、DA的中点,求SEFGH.