题目内容
2．若定义域为R的函数f（x）的周期为2，当x∈（-1，1]时，f（x）=|x|，则函数y=f（x）的图象与y=log3|x|的图象的交点个数为（ ）| A． | 8 | B． | 6 | C． | 4 | D． | 2 |
分析 根据函数的周期性作出函数f（x）和y=log3|x|的图象，利用数形结合即可得到结论．
解答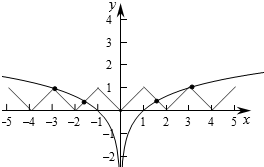 
解：∵函数y=f（x）的周期为2，当x∈（-1，1]时，f（x）=，
∴f（3）=f（1）=1，
当x=±3时，函数y=log3|x|=log33=1，
作出函数f（x）和y=log3|x|的图象如图：
由图象可知两个函数的图象交点为4个，
故选：C
点评 本题主要考查函数交点个数的判断，利用函数的周期性作出函数图象，利用数形结合是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
12．某班40个学生平均分成两组，两组学生某次考试的成绩情况如下表所示：
求这次考试全班的平均成绩和标准差．（ 注：平均数$\overline{x}=\frac{{{x_1}+{x_2}+…+{x_n}}}{n}$，
标准差$s=\sqrt{\frac{1}{n}[{（{x_1}-{{\overline{x）}}^2}+{{（{x_2}-\bar\overline{x}）}^2}+…+{{（{x_n}-\bar\overline{x}）}^2}}]}=\sqrt{\frac{1}{n}[{（x_1^2+x_2^2+…+x_n^2）-n{{\bar\overline{x}}^2}}]}$）
| 组别 | 平均数 | 标准差 |
| 第一组 | 90 | 4 |
| 第二组 | 80 | 6 |
标准差$s=\sqrt{\frac{1}{n}[{（{x_1}-{{\overline{x）}}^2}+{{（{x_2}-\bar\overline{x}）}^2}+…+{{（{x_n}-\bar\overline{x}）}^2}}]}=\sqrt{\frac{1}{n}[{（x_1^2+x_2^2+…+x_n^2）-n{{\bar\overline{x}}^2}}]}$）
17．为了得到函数y=cosx，x∈R的图象，只需把y=cos$\frac{x}{5}$，x∈R上所有的点的（ ）
| A． | 横坐标伸长为原来的5倍，纵坐标不变 | |
| B． | 横坐标缩短为原来的$\frac{1}{5}$倍，纵坐标不变 | |
| C． | 纵坐标伸长为原来的5倍，横坐标不变 | |
| D． | 纵坐标缩短为原来的$\frac{1}{5}$倍，横坐标不变 |
14．已知复数z满足（1+i）z=1则z在复平面内对应的点位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
一艘海轮从A处出发，以40n mile/h的速度沿南偏东40°方向直线航行，30min后到达B处，在C处有一座灯塔，海轮在A处观察灯塔，其方向是南偏东70°，在B处观察灯塔，其方向是北偏东65°，那么B，C两点间的距离是10$\sqrt{2}$n mile．