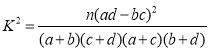题目内容
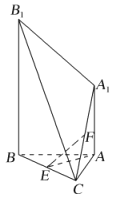
【题目】如图,已知![]() 平面ABC,
平面ABC,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点E和F分别为BC和
,点E和F分别为BC和![]() 的中点.
的中点.
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:直线![]() 平面
平面![]() ;
;
(3)求直线![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)连接![]() ,由题意易知
,由题意易知![]() ,再由线面平行的判定定理可得出结论;(2)结合题中条件利用线面垂直的判定定理直接判断即可证明结论;(3)分别取
,再由线面平行的判定定理可得出结论;(2)结合题中条件利用线面垂直的判定定理直接判断即可证明结论;(3)分别取![]() 的中点M,N,连接
的中点M,N,连接![]() ,
,![]() ,利用题中相关已知条件即可证明
,利用题中相关已知条件即可证明![]() ,利用(2)的结论可得
,利用(2)的结论可得![]() 面
面![]() ,则可得
,则可得![]() 就是直线
就是直线![]() 与平面
与平面![]() 所成的角,再结合题中数量关系可求得
所成的角,再结合题中数量关系可求得![]() =4,
=4,![]() ,则在
,则在![]() 中可得
中可得![]() ,则可得
,则可得![]() .
.
(1)证明:
如图,连接![]() ,
,
在![]() 中,因为E和F分别是BC和
中,因为E和F分别是BC和![]() 的中点,所以
的中点,所以![]() .
.
又因为EF平面![]() ,
,![]() 平面
平面![]() ,所以
,所以平面
![]() .
.
(2)证明:
因为![]() ,E为BC的中点,所以
,E为BC的中点,所以![]() .因为
.因为![]() 平面ABC,
平面ABC,![]() ,所以
,所以![]() 平面ABC,又
平面ABC,又![]() 平面ABC,从而
平面ABC,从而![]() .又因为
.又因为![]() ,
,
所以![]() 平面
平面![]() .
.
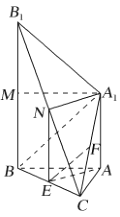
(3)解:取![]() 的中点M和
的中点M和![]() 的中点N,连接
的中点N,连接![]() ,
,![]() ,NE.因为N和E分别为
,NE.因为N和E分别为![]() 和BC的中点,所以
和BC的中点,所以![]() ,
,![]() ,故
,故![]() 且
且![]() ,所以
,所以![]() ,且
,且![]() .又因为
.又因为![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
从而![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角.
所成的角.
在![]() 中,可得
中,可得![]() ,所以
,所以![]() .
.
因为![]() ,
,![]() ,
,
所以四边形![]() 为平行四边形,
为平行四边形,
所以![]() ,
,![]() ,
,
又由![]() ,得
,得![]() .
.
在![]() 中,
中,
可得![]() .
.
在![]() 中,
中,
![]()
因此![]() .
.
所以直线![]() 与平面
与平面![]() 所成的角为30°.
所成的角为30°.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案【题目】为了调查某生产线上质量监督员甲是否在现场对产品质量好坏有无影响,现统计数据如下:质量监督员甲在现场时,1 000件产品中合格品有990件,次品有10件,甲不在现场时,500件产品中有合格品490件,次品有10件.
(1)补充下面列联表,并初步判断甲在不在现场与产品质量是否有关:
合格品数/件 | 次品数/件 | 总数/件 | |
甲在现场 | 990 | ||
甲不在现场 | 10 | ||
总数/件 |
(2)用独立性检验的方法判断能否在犯错误的概率不超过0.15的前提下认为“甲在不在现场与产品质量有关”?
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |