Question

【题目】已知抛物线，焦点为，过点的直线交抛物线于，两点，则的最小值为__________．

Answer 1

【答案】

【解析】分析：设A（x1，y1），B（x2，y2）．当直线AB的斜率存在时，设直线AB的方程为y=k（x﹣），（k≠0）．与抛物线方程联立可得根与系数的关系，利用|AF|+4|BF|=x1++2（x2+）及其基本不等式的性质即可得出，当直线AB的斜率不存在时，直接求出即可．

详解：F（，0），

设A（x1，y1），B（x2，y2）．

当直线AB的斜率存在时，设直线AB的方程为y=k（x﹣），（k≠0）．

联立 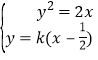，化为k2x2﹣（k2+2）x+k2=0．

x1x2=．

∴|AF|+2|BF|=x1++2（x2+）=x1+2x2+≥2+=，当且仅当x1=2x2=时取等号．

当直线AB的斜率不存在时，|AF|+2|BF|=3p=3．

综上可得：|AF|+2|BF|的最小值为：．

故答案为：．