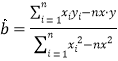题目内容
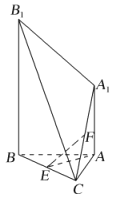
【题目】在如图所示的几何体中,![]() 平面
平面![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)过点![]() 作一平行于平面
作一平行于平面![]() 的截面,画出该截面,说明理由,并求夹在该截面与平面
的截面,画出该截面,说明理由,并求夹在该截面与平面![]() 之间的几何体的体积.
之间的几何体的体积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】分析:(1)由余弦定理结合勾股定理可证明![]() ,利用线面垂直的性质可证明
,利用线面垂直的性质可证明![]() ,由线面垂直的判定定理可得
,由线面垂直的判定定理可得![]() 平面
平面![]() ;(2)取
;(2)取![]() 的中点
的中点![]() ,
,![]() 的中点
的中点![]() ,连接
,连接![]() ,截面
,截面![]() 即为所求,由(1)可知,
即为所求,由(1)可知,![]() 平面
平面![]() ,
,![]() 平面
平面![]() , 由“分割法”利用棱锥的体积公式可得结果.
, 由“分割法”利用棱锥的体积公式可得结果.
详解:(1)证明:在![]() 中,
中,![]() .
.
所以![]() ,所以
,所以![]() 为直角三角形,
为直角三角形,![]() .
.
又因为![]() 平面
平面![]() ,所以
,所以![]() .
.
而![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)取![]() 的中点
的中点![]() ,
,![]() 的中点
的中点![]() ,连接
,连接![]() ,平面
,平面![]() 即为所求.
即为所求.
理由如下:
因为![]() ,所以四边形
,所以四边形![]() 为平行四边形,所以
为平行四边形,所以![]() ,从而
,从而![]() 平面
平面![]() ,
,
同理可证![]() 平面
平面![]() .
.
因为![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
由(1)可知,![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
因为![]() ,
,
![]() ,
,
所以,所求几何体的体积![]() .
.

练习册系列答案
相关题目
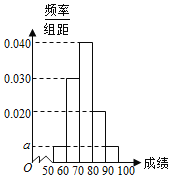
【题目】某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图![]() 如图所示
如图所示![]() ,规定80分及以上者晋级成功,否则晋级失败.
,规定80分及以上者晋级成功,否则晋级失败.
晋级成功 | 晋级失败 | 合计 | |
男 | 16 | ||
女 | 50 | ||
合计 |
![]() Ⅰ
Ⅰ![]() 求图中a的值;
求图中a的值;
![]() Ⅱ
Ⅱ![]() 根据已知条件完成下面
根据已知条件完成下面![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为“晋级成功”与性别有关?
的把握认为“晋级成功”与性别有关?
![]() Ⅲ
Ⅲ![]() 将频率视为概率,从本次考试的所有人员中,随机抽取4人进行约谈,记这4人中晋级失败的人数为X,求X的数学期望
将频率视为概率,从本次考试的所有人员中,随机抽取4人进行约谈,记这4人中晋级失败的人数为X,求X的数学期望![]() 与方差
与方差![]() .
.
![]() 参考公式:
参考公式:![]() ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|