题目内容
已知函数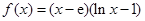
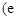 为自然对数的底数).
为自然对数的底数).
(1)求曲线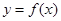 在
在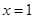 处的切线方程;
处的切线方程;
(2)若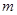 是
是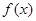 的一个极值点,且点
的一个极值点,且点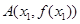 ,
,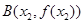 满足条件:
满足条件: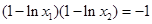 .
.
(ⅰ)求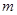 的值;
的值;
(ⅱ)若点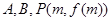 是三个不同的点, 判断
是三个不同的点, 判断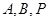 三点是否可以构成直角三
三点是否可以构成直角三
角形?请说明理由。
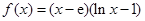
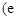 为自然对数的底数).
为自然对数的底数).(1)求曲线
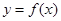 在
在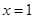 处的切线方程;
处的切线方程;(2)若
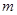 是
是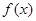 的一个极值点,且点
的一个极值点,且点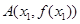 ,
,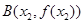 满足条件:
满足条件: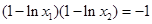 .
.(ⅰ)求
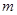 的值;
的值;(ⅱ)若点
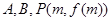 是三个不同的点, 判断
是三个不同的点, 判断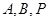 三点是否可以构成直角三
三点是否可以构成直角三角形?请说明理由。
(1) ;(2)
;(2) ;点
;点 ,
, ,
, 可构成直角三角形.
可构成直角三角形.
 ;(2)
;(2) ;点
;点 ,
, ,
, 可构成直角三角形.
可构成直角三角形.试题分析:本题主要考查导数的运算、利用导数求曲线的切线方程、利用导数判断函数的单调性、利用导数求函数的最值和极值、向量垂直的充要条件等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,对
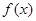 求导,将切点的横坐标1代入到
求导,将切点的横坐标1代入到 中得到切线的斜率,代入到
中得到切线的斜率,代入到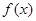 中得到切点的纵坐标,从而利用点斜式得到切线方程;第二问,先求函数的定义域,令
中得到切点的纵坐标,从而利用点斜式得到切线方程;第二问,先求函数的定义域,令 ,得到方程的根,将定义域断开,判断函数的单调性,从而求出函数极值;第三问,先排除几个特例情况,在一般情况中,要证明三角形为直角三角形,只需判断2边垂直,用向量垂直的充要条件证明即可.
,得到方程的根,将定义域断开,判断函数的单调性,从而求出函数极值;第三问,先排除几个特例情况,在一般情况中,要证明三角形为直角三角形,只需判断2边垂直,用向量垂直的充要条件证明即可.试题解析:(1)
 ,
,  ,又
,又 ,所以曲线
,所以曲线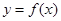 在
在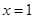 处的切线方程为
处的切线方程为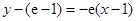 ,即
,即 .
.(2)(ⅰ)对于
 ,定义域为
,定义域为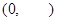 .
.当
 时,
时, ,
, ,∴
,∴ ;
;当
 时,
时,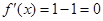 ;当
;当 时,
时,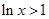 ,
, ,∴
,∴
所以
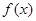 存在唯一的极值点
存在唯一的极值点 ,∴
,∴ ,则点
,则点 为
为
(ⅱ)若
 ,则
,则 ,与条件
,与条件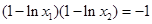 不符,
不符,从而得
 .同理可得
.同理可得 .
.若
 ,则
,则 ,与条件
,与条件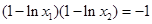 不符,从而得
不符,从而得 .
. 由上可得点
 ,
, ,
, 两两不重合.
两两不重合.



从而
 ,点
,点 ,
, ,
, 可构成直角三角形.
可构成直角三角形.
练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
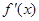 ,且满足
,且满足 ,则
,则 与
与 的大小关系为( ).
的大小关系为( ).
 若当0
若当0 时,
时, 恒成立,则实数m的取值范围是 ( )
恒成立,则实数m的取值范围是 ( )
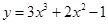 在区间
在区间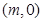 上为减函数, 则
上为减函数, 则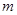 的取值范围是__ ___.
的取值范围是__ ___. 内不是增函数的是( )
内不是增函数的是( )



 在
在 上单调递增,则实数
上单调递增,则实数 的取值范围是 .
的取值范围是 .