题目内容
在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,E为PC中点,底 面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=1,CD=2.
(Ⅰ)求证:BE∥平面PAD;
(Ⅱ)求证:BC⊥平面PBD;
(Ⅲ)求四棱锥P-ABCD的体积。
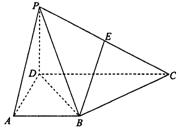
(Ⅰ)求证:BE∥平面PAD;
(Ⅱ)求证:BC⊥平面PBD;
(Ⅲ)求四棱锥P-ABCD的体积。

解:(Ⅰ)证明:取PD的中点F,连结EF,AF,
因为E为PC中点,所以EF∥CD,且EF=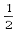 CD=1,
CD=1,
在梯形ABCD中,AB∥CD,AB=1,
所以EF∥AB,EF=AB,四边形ABEF为平行四边形,
所以BE∥AF,
又∵ BE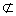 平面PAD,AF
平面PAD,AF 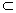 平面PAD, 所以BE∥平面PAD
平面PAD, 所以BE∥平面PAD
(2)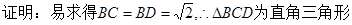
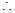 BC⊥BD,又BC⊥PD,
BC⊥BD,又BC⊥PD,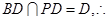 BC⊥平面PBD
BC⊥平面PBD
(3)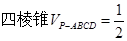
因为E为PC中点,所以EF∥CD,且EF=
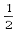 CD=1,
CD=1,在梯形ABCD中,AB∥CD,AB=1,
所以EF∥AB,EF=AB,四边形ABEF为平行四边形,
所以BE∥AF,
又∵ BE
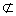 平面PAD,AF
平面PAD,AF 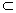 平面PAD, 所以BE∥平面PAD
平面PAD, 所以BE∥平面PAD (2)
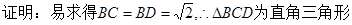
 BC⊥BD,又BC⊥PD,
BC⊥BD,又BC⊥PD,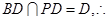 BC⊥平面PBD
BC⊥平面PBD (3)
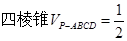
本试题主要考查了线面平行和线面垂直的判定定理和四棱锥的体积的综合运用。
(1)先找到线线平行,BE∥AF,从而利用判定定理得到结论。
(2)要证明线面垂直,先证明线线垂直,利用判定定理得到结论。
(3)对于体积的求解关键是求解底面积和体的高,然后得到结论。
(1)先找到线线平行,BE∥AF,从而利用判定定理得到结论。
(2)要证明线面垂直,先证明线线垂直,利用判定定理得到结论。
(3)对于体积的求解关键是求解底面积和体的高,然后得到结论。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
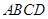 所在平面与三角形
所在平面与三角形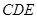 所在平面相交于
所在平面相交于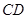 ,
,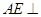 平面
平面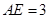 ,
,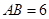
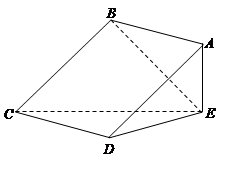
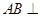 平面
平面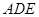 ;
;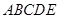 的体积.
的体积.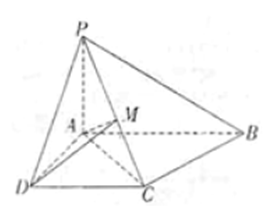
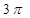
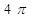
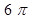

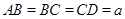 ,
,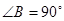 ,
,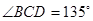 ,沿对角线
,沿对角线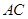 将
将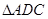 折起,使面
折起,使面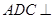 面
面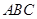 ,
,
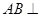 面
面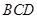 ;
;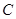 到面
到面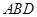 的距离.
的距离.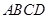 的外接球的球心为
的外接球的球心为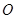 ,
,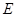 是
是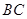 的中点,则直线
的中点,则直线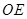 和平面
和平面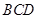 所成角的正切值为 。
所成角的正切值为 。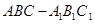 中,侧棱垂直于底面,底面是边长为2的正三角形,侧棱长为3,则
中,侧棱垂直于底面,底面是边长为2的正三角形,侧棱长为3,则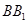 与平面
与平面 所成的角的大小为
所成的角的大小为 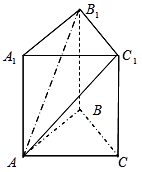
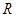 的球内部装4个有相同半径
的球内部装4个有相同半径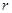 的小球,则小球半径
的小球,则小球半径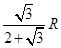
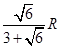
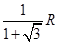
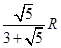
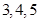 ,则这个长方体的对角线长为__________
,则这个长方体的对角线长为__________