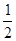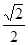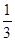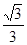题目内容
如图,在三棱柱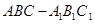 中,侧棱垂直于底面,底面是边长为2的正三角形,侧棱长为3,则
中,侧棱垂直于底面,底面是边长为2的正三角形,侧棱长为3,则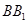 与平面
与平面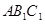 所成的角的大小为
所成的角的大小为 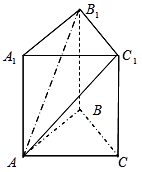
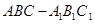 中,侧棱垂直于底面,底面是边长为2的正三角形,侧棱长为3,则
中,侧棱垂直于底面,底面是边长为2的正三角形,侧棱长为3,则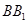 与平面
与平面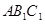 所成的角的大小为
所成的角的大小为 
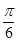
解:以B为坐标原点,以与BC垂直的直线为x轴,BC为y轴,建立空间直角坐标系,
则A( 3 ,1,0),B1(0,0,3),C1(0,2,3), AB1 =(- 3 ,-1,3), B1C1 =(0,2,0), BB1 =(0,0,3).
设平面AB1C1所的一个法向量为 n =(x,y,z)
则 AB1 • n =0 B1C1 • n =0 即 - 3 x-y+3z="0" 2y=0 ,取z=1,则得 n =(- 3 ,0,1),
∵cos< BB1, n >= (BB1• n)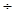 ( | BB1 || n |) ="1"
( | BB1 || n |) ="1" 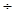 2 ,
2 ,
∴BB1与平面AB1C1所成的角的正弦值为1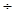 2 ,
2 ,
∴BB1与平面AB1C1所成的角为π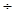 6
6
则A( 3 ,1,0),B1(0,0,3),C1(0,2,3), AB1 =(- 3 ,-1,3), B1C1 =(0,2,0), BB1 =(0,0,3).
设平面AB1C1所的一个法向量为 n =(x,y,z)
则 AB1 • n =0 B1C1 • n =0 即 - 3 x-y+3z="0" 2y=0 ,取z=1,则得 n =(- 3 ,0,1),
∵cos< BB1, n >= (BB1• n)
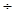 ( | BB1 || n |) ="1"
( | BB1 || n |) ="1" 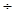 2 ,
2 ,∴BB1与平面AB1C1所成的角的正弦值为1
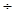 2 ,
2 ,∴BB1与平面AB1C1所成的角为π
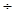 6
6 
练习册系列答案
相关题目
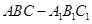 中,
中,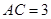 ,
,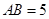 ,
,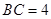
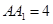 ,点
,点 是
是 的中点.
的中点.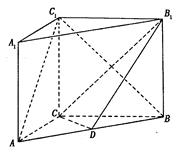
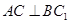 ;
;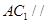 平面
平面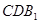 ;
;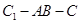 的正切值.
的正切值.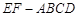 中,
中, 是梯形,
是梯形,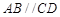 ,
, 是矩形,平面
是矩形,平面 平面
平面 ,
,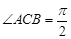 .
.
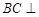 平面
平面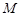 是棱
是棱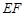 上一点,
上一点,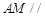 平面
平面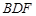 ,求
,求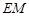 ;
;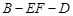 的平面角的余弦值.
的平面角的余弦值.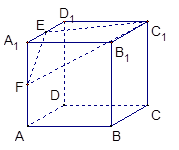
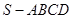 的底面为正方形,
的底面为正方形,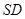 ⊥底面
⊥底面 ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )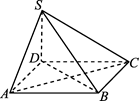

 平面
平面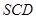
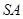 与平面
与平面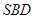 所成的角等于
所成的角等于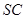 与平面
与平面 与
与 与
与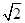 、
、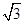 ,则此三棱锥的外接球的表面积是____________.
,则此三棱锥的外接球的表面积是____________.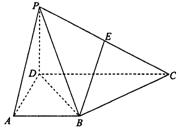
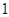 的正四面体
的正四面体 中,若
中,若 、
、 分别是棱
分别是棱 、
、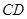 的中点,则
的中点,则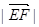 =
=