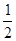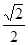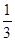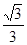题目内容
如图,已知四棱锥P—ABCD中,底面ABCD是直角梯长,AB//CD,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1。
(1)求证:BC⊥平面PAC;
(2)若M是PC的中点,求三棱锥M—ACD的体积。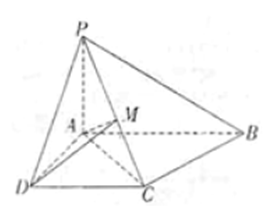
(1)求证:BC⊥平面PAC;
(2)若M是PC的中点,求三棱锥M—ACD的体积。

(1)见解析;(2)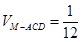
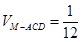
本试题主要是考查了立体几何中线面垂直的判定定理和锥体体积公式的运用。
(1)因为在直角梯形ABCD中,过C做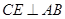 于点E,则四边形ADCE为矩形,关键是证明
于点E,则四边形ADCE为矩形,关键是证明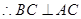 ,得到线面垂直。
,得到线面垂直。
(2)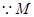 是PC中点
是PC中点
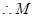 到面ADC的距离是P到面ADC距离的一半,从而得到高度,结合底面积得到体积。
到面ADC的距离是P到面ADC距离的一半,从而得到高度,结合底面积得到体积。
解:(1)证明:在直角梯形ABCD中,过C做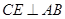 于点E,则四边形ADCE为矩形
于点E,则四边形ADCE为矩形

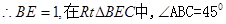 …3分
…3分
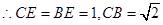 …………4分
…………4分
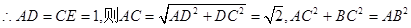
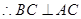 …………6分
…………6分
又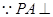 平面ABCD,
平面ABCD,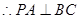 ……7分
……7分
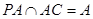 ,
,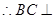 平面APC…………9分
平面APC…………9分
(2)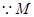 是PC中点
是PC中点
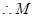 到面ADC的距离是P到面ADC距离的一半…………10分
到面ADC的距离是P到面ADC距离的一半…………10分
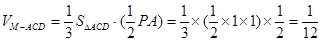 …………12分
…………12分
(1)因为在直角梯形ABCD中,过C做
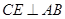 于点E,则四边形ADCE为矩形,关键是证明
于点E,则四边形ADCE为矩形,关键是证明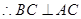 ,得到线面垂直。
,得到线面垂直。(2)
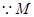 是PC中点
是PC中点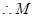 到面ADC的距离是P到面ADC距离的一半,从而得到高度,结合底面积得到体积。
到面ADC的距离是P到面ADC距离的一半,从而得到高度,结合底面积得到体积。解:(1)证明:在直角梯形ABCD中,过C做
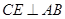 于点E,则四边形ADCE为矩形
于点E,则四边形ADCE为矩形
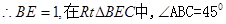 …3分
…3分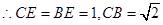 …………4分
…………4分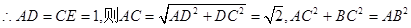
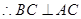 …………6分
…………6分又
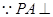 平面ABCD,
平面ABCD,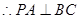 ……7分
……7分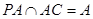 ,
,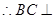 平面APC…………9分
平面APC…………9分(2)
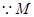 是PC中点
是PC中点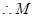 到面ADC的距离是P到面ADC距离的一半…………10分
到面ADC的距离是P到面ADC距离的一半…………10分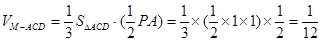 …………12分
…………12分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
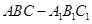 中,
中,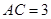 ,
,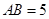 ,
,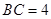
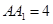 ,点
,点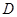 是
是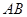 的中点.
的中点.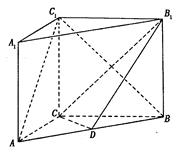
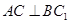 ;
;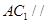 平面
平面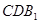 ;
;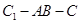 的正切值.
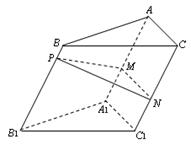
的正切值.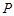 为斜三棱柱
为斜三棱柱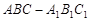 的侧棱
的侧棱 上一点,
上一点,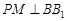 交
交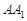 于点
于点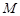 ,
,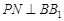 交
交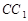 于点
于点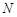 .
.
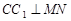 ;
;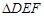 中有余弦定理:
中有余弦定理: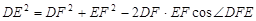 . 拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式(只写结论,不必证明)
. 拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式(只写结论,不必证明)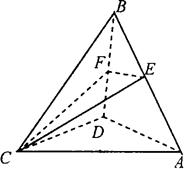
 ,从长方体的一条对角线的一个
,从长方体的一条对角线的一个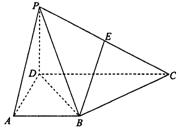
 的正四面体
的正四面体 中,若
中,若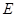 、
、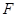 分别是棱
分别是棱 、
、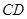 的中点,则
的中点,则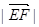 =
=