题目内容
在△ 中,角
中,角 、
、 、
、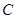 所对的边分别为
所对的边分别为 、
、 、
、 ,已知
,已知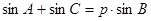 (
(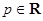 ),且
),且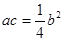 .
.
(1)当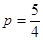 ,
,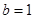 时,求
时,求 ,
, 的值;
的值;
(2)若 为锐角,求实数
为锐角,求实数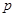 的取值范围.
的取值范围.
(1)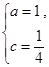 或
或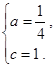 ;(2)
;(2)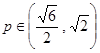 .
.
解析试题分析:(1)题设要求边,因此已知中角的关系应该转化为边的关系,显然应用正弦定理可达到目的, ,再由已知
,再由已知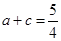 ,与
,与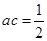 联立可解得
联立可解得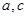 ;(2)已知
;(2)已知 为锐角,即
为锐角,即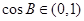 ,因此为了求
,因此为了求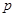 的范围,最好能把
的范围,最好能把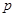 用
用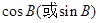 表示出来,首先用余弦定理
表示出来,首先用余弦定理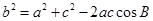
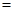
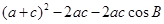 ,把已知条件代入,可得所想要的关系式
,把已知条件代入,可得所想要的关系式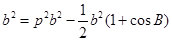 ,即
,即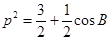 ,由此可求得范围.
,由此可求得范围.
试题解析:(1)由正弦定理得,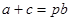 ,所以
,所以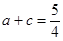 , (2分)
, (2分)
又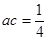 ,所以
,所以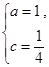 或
或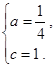 (5分)(少一组解扣1分)
(5分)(少一组解扣1分)
(2)由余弦定理,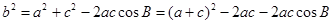 ,(1分)
,(1分)
即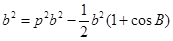 , (2分)
, (2分)
所以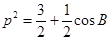 . (4分)
. (4分)
由 是锐角,得
是锐角,得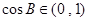 ,所以
,所以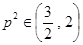 . (6分)
. (6分)
由题意知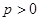 ,所以
,所以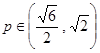 . (7分)
. (7分)
考点:(1)正弦定理;(2)余弦定理及三角函数值的范围.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
 、
、 、
、 、
、 ,欲测量
,欲测量 米,如图,同时也能测量出
米,如图,同时也能测量出 ,
, ,
,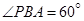 ,
, ,则
,则
 ,
, 

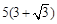 海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距
海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距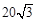 海里的C点的救援船立即即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
海里的C点的救援船立即即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
 中,
中,
 的值;
的值;
 ,b+c=3,求△ABC的面积.
,b+c=3,求△ABC的面积. .
. 的单调增区间;
的单调增区间; 中,
中,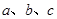 分别是角
分别是角 的对边,且
的对边,且 ,求
,求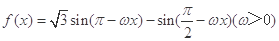 的图像上两相邻最高点的坐标分别为
的图像上两相邻最高点的坐标分别为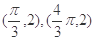 .
. 的值;
的值;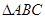 中,
中,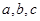 分别是角
分别是角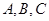 的对边,且
的对边,且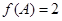 ,求
,求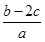 的取值范围.
的取值范围.