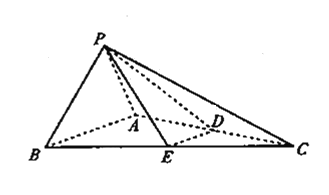
题目内容
【题目】设![]() 是由
是由![]() 个有序实数构成的一个数组,记作:
个有序实数构成的一个数组,记作:![]() .其中
.其中![]() 称为数组
称为数组![]() 的“元”,
的“元”,![]() 称为
称为![]() 的下标,如果数组
的下标,如果数组![]() 中的每个“元”都是来自数组
中的每个“元”都是来自数组![]() 中不同下标的“元”,则称
中不同下标的“元”,则称![]() 为
为![]() 的子数组.定义两个数组
的子数组.定义两个数组![]() ,
,![]() 的关系数为
的关系数为![]() .
.
(1)若![]() ,
,![]() ,设
,设![]() 是
是![]() 的含有两个“元”的子数组,求
的含有两个“元”的子数组,求![]() 的最大值;
的最大值;
(2)若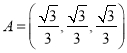 ,
,![]() ,且
,且![]() ,
,![]() 为
为![]() 的含有三个“元”的子数组,求
的含有三个“元”的子数组,求![]() 的最大值;
的最大值;
(3)若数组![]() 中的“元”满足
中的“元”满足![]() ,设数组
,设数组![]() 含有四个“元”
含有四个“元”![]() ,且
,且![]() ,求
,求![]() 与
与![]() 的所有含有三个“元”的子数组的关系数
的所有含有三个“元”的子数组的关系数![]() (
(![]() )的最大值.
)的最大值.
【答案】(1)2(2)1(3)![]()
【解析】
(1)根据题中“元”的定义,列出所有![]() 的含有两个“元”的子数组,当取到
的含有两个“元”的子数组,当取到![]() 时,取到最大值;
时,取到最大值;
(2)需要进行分类讨论,分为![]() 中含0和不含0这个“元”两种具体情况进行分类讨论,再结合不等式性质进行合理放缩即可求得最值;
中含0和不含0这个“元”两种具体情况进行分类讨论,再结合不等式性质进行合理放缩即可求得最值;
(3)可以借鉴(2)中解题方法,分为![]() 和
和![]() 两种情况,再结合基本不等式性质经行求解即可
两种情况,再结合基本不等式性质经行求解即可
(1)由题,列出所有符合题意的子数组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,由定义
,由定义![]() ,
,![]() ,计算可得,当
,计算可得,当![]() 时,
时,![]() ;
;
(2)由![]() ,
,![]() 可知,实数
可知,实数![]() 具有对称性,故分为
具有对称性,故分为![]() 中含0和不含0这个“元”两种具体情况进行分类讨论;
中含0和不含0这个“元”两种具体情况进行分类讨论;
①当0是![]() 中的“元”时,由于
中的“元”时,由于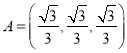 中的三个“元”都相等及
中的三个“元”都相等及![]() 中三个“元”
中三个“元”![]() 的对称性,可只计算
的对称性,可只计算![]() 的最大值,
的最大值,![]() ,
,
由![]() 可得
可得![]() ,
,
故当![]() 时
时![]() 达到最大值
达到最大值![]() ,故
,故![]() ;
;
②当不是![]() 中的“元”时,
中的“元”时,
![]()
又![]() ,根据同向可加性可得
,根据同向可加性可得
![]() ,即
,即![]() ,则
,则
![]() ,当且仅当
,当且仅当![]() 时,取到最大值,故
时,取到最大值,故![]() ;
;
综上所述,![]() ;
;
(3)解法和(2)接近,![]() ,
,![]() ,根据
,根据![]() 及
及
![]() 的对称性,分为
的对称性,分为![]() 和
和![]() 两种情况进行求解;
两种情况进行求解;
当![]() 时,为了保证不等式的等价性,需对
时,为了保证不等式的等价性,需对![]() 做变形处理,得
做变形处理,得
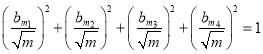 ,此时
,此时
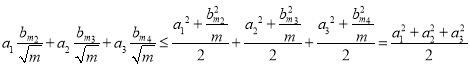
![]() ,当且仅当
,当且仅当![]() 时等号成立;
时等号成立;
![]()
![]() ;
;
当![]() 时,
时,![]() ,此时,
,此时,![]()
综上所述,![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目