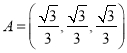题目内容
【题目】椭圆![]() 将圆
将圆![]() 的圆周分为四等份,且椭圆
的圆周分为四等份,且椭圆![]() 的离心率为
的离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,且
,且![]() 的中点为
的中点为![]() ,线段
,线段![]() 的垂直平分线为
的垂直平分线为![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)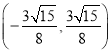
【解析】
(1)先求解A点坐标,代入椭圆方程,结合离心率为![]() ,即得解.
,即得解.
(2)设![]() ,
,![]() ,利用点差法得到
,利用点差法得到![]() ,得到直线
,得到直线![]() 的方程为
的方程为![]() ,得到
,得到![]() ,利用
,利用![]() 在椭圆内部得到
在椭圆内部得到![]() 范围,即得解.
范围,即得解.
(1)不妨取第一象限的交点为![]() .
.
由椭圆![]() 将圆
将圆![]() 的圆周分为四等份,知
的圆周分为四等份,知![]() .
.
所以 .
.
因为点![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() .①
.①
因为![]() ,所以
,所以![]() .②
.②
①②联立,解得![]() ,
,![]() .
.
所以椭圆![]() 的方程为
的方程为![]() .
.
(2)设![]() ,
,![]() ,则
,则
两式相减,得![]() .
.
又因![]() 的中点为
的中点为![]() ,所以
,所以![]() ,
,![]() .
.
所以直线![]() 的斜率
的斜率![]() .
.
当![]() 时,直线
时,直线![]() 的方程
的方程![]() ,直线
,直线![]() 即
即![]() 轴,此时
轴,此时![]() .
.
当![]() 时,直线
时,直线![]() 的斜率
的斜率![]() .
.
所以直线![]() 的方程为
的方程为![]() ,即
,即![]() .
.
令![]() ,则
,则![]() .
.
因为点![]() 在椭圆内部,所以
在椭圆内部,所以![]() .
.
所以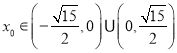 ,所以
,所以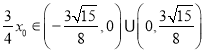 .
.
综上所述,![]() 的取值范围为
的取值范围为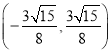 .
.

练习册系列答案
相关题目