题目内容
12.已知函数f(x)=x2+bx+c-2,若关于x的不等式-2≤f(x)≤2的解集为[x1,x2]∪[x3,x4](x2<x3),则W=(2x4-x3)-(2x1-x2)的最小值为4$\sqrt{3}$.分析 由题意可知f(x1)=f(x4)=2,f(x2)=f(x3)=-2,利用跟与系数的关系可用b,c表示出x4-x1,x2-x3,
将W化简为2$\sqrt{{b}^{2}-4c+16}$-$\sqrt{{b}^{2}-4c}$,令$\sqrt{{b}^{2}-4c}$=t,然后使用换元法求出W的最小值.
解答 解:∵-2≤f(x)≤2的解集为[x1,x2]∪[x3,x4](x2<x3),
∴f(x1)=f(x4)=2,
f(x2)=f(x3)=-2,
即x1,x4是方程x2+bx+c-4=0的两根,
x2,x3是方程x2+bx+c=0的两根.
∴x1+x4=-b,x1x4=c-4.
x2+x3=-b,x2x3=c.
且b2-4c>0.
∵(x4-x1)2=(x4+x1)2-4x4x1=b2-4c+16,
(x2-x3)2=(x2+x3)2-4x2x3=b2-4c.
∴x4-x1=$\sqrt{{b}^{2}-4c+16}$,
x2-x3=-$\sqrt{{b}^{2}-4c}$.
∴W=(2x4-x3)-(2x1-x2)=2(x4-x1)+x2-x3
=2$\sqrt{{b}^{2}-4c+16}$-$\sqrt{{b}^{2}-4c}$.
令$\sqrt{{b}^{2}-4c}$=t,则t>0
∴W(t)=2$\sqrt{t+16}$-$\sqrt{t}$,
W′(t)=$\frac{1}{\sqrt{t+16}}$-$\frac{1}{2\sqrt{t}}$.
令W′(t)=0得$\sqrt{t+16}$=2$\sqrt{t}$,解得t=$\frac{16}{3}$.
当0<t<$\frac{16}{3}$时,W′(t)<0;当t>$\frac{16}{3}$时,W′(t)>0.
∴当t=$\frac{16}{3}$时,W(t)取得最小值W($\frac{16}{3}$)=2$\sqrt{\frac{16}{3}+16}$-$\sqrt{\frac{16}{3}}$=4$\sqrt{3}$.
故答案为4$\sqrt{3}$.
点评 本题考查了一元二次不等式,换元法及导数的应用,属于综合题.

 阅读快车系列答案
阅读快车系列答案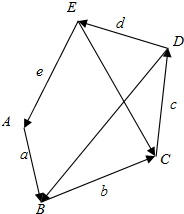 向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,$\overrightarrow{d}$,$\overrightarrow{e}$如图所示,解答下列各题:
向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,$\overrightarrow{d}$,$\overrightarrow{e}$如图所示,解答下列各题: