Question

6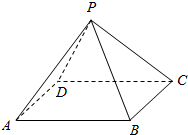．如图，P-ABCD是一个各棱长都为2cm的正四棱锥，求这个棱锥的表面积和体积．

Answer 1

分析 要求正四棱锥P-ABCD的体积我们要根据底边长为2计算出底面积，然后根据底边长为2、侧棱长为2．求出棱锥的高，代入即可求出体积；要求侧面积，我们还要计算出侧高，进而得到棱锥的侧面积．

解答 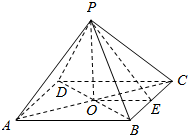解：设底面ABCD的中心为O，边BC中点为E，
连接PO，PE，OE（1分）
在Rt△PEB．
中，PB=2，
BE=1，则斜高PE=$\sqrt{3}$（2分）
在Rt△POE
中，PE=$\sqrt{3}$，
OE=1，则高PO=$\sqrt{2}$（4分）
所以V=$\frac{1}{3}$•S_ABCD•PO=$\frac{1}{3}×2×2×\sqrt{2}$=$\frac{4\sqrt{2}}{3}$（6分）
S_侧面积=4×$\frac{1}{2}$×$2×\sqrt{3}$=4$\sqrt{3}$（8分）．
S_表=4+4$\sqrt{3}$

点评 本题考查的知识点是棱锥的体积和表面积，其中树立求体积先求棱锥的高，求表面积先求棱锥的侧高，是解答本题的关键．