题目内容
9.用斜二侧画法画一个周长为4的矩形的直观图,试求直观图面积的最大值.分析 在已知图形所在的空间中取水平平面,作X′轴,Y′轴使∠X′O′Y′=45°,然后依据平行投影的有关性质逐一作图.利用基本不等式求直观图面积的最大值.
解答 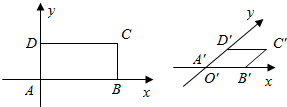 解:(1)在已知ABCD中取AB、AD所在边为X轴与Y轴,相交于O点(O与A重合),画对应X′轴,Y′轴使∠X′O′Y′=45°
解:(1)在已知ABCD中取AB、AD所在边为X轴与Y轴,相交于O点(O与A重合),画对应X′轴,Y′轴使∠X′O′Y′=45°
(2)在X′轴上取A′,B′使A′B′=AB,在Y′轴上取D′,
使A′D′=$\frac{1}{2}$AD,过D′作D′C′平行X′的直线,且等于A′D′长.
(3)连C′B′所得四边形A′B′C′D′就是矩形ABCD的直观图.
设矩形的长、宽分别为a,b,则a+b=2≥2$\sqrt{ab}$,
∴ab≤1,∴直观图面积的最大值为1.
点评 本题考查平面图形的直观图的画法:斜二测画法,考查作图能力,属基础知识的考查.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
11.已知点F(c,0)(c>0)是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的右焦点,F关于直线y=$\sqrt{3}$x的对称点A也在该椭圆上,则该椭圆的离心率是( )
| A. | $\sqrt{3}$+2 | B. | $\sqrt{3}$-1 | C. | -$\sqrt{3}$+1 | D. | -$\sqrt{3}$+2 |
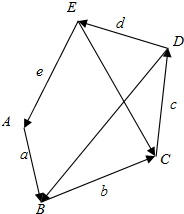 向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,$\overrightarrow{d}$,$\overrightarrow{e}$如图所示,解答下列各题:
向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,$\overrightarrow{d}$,$\overrightarrow{e}$如图所示,解答下列各题: