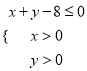Question

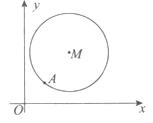
【题目】如图，在平面直角坐标系中，已知以为圆心的圆及其上一点.

（1）是否存在直线与圆有两个交点，并且，若有，求此直线方程，若没有，请说明理由；

（2）设点满足：存在圆上的两点和使得，求实数的取值范围.

Answer 1

【答案】(1)答案见解析；(2) .

【解析】试题分析：

(1)假设存在满足题意的直线，结合题意和假设可得直线与圆相离的矛盾，即不存在满足题意的直线；

(2)由题意得到关于实数t的不等式，求解不等式可得实数的取值范围是.

试题解析：

(1)由已知，可知直线， 直线为，即，又圆心到直线的距离，即直线与圆相离，所以不存在.

(2)设， ， ①

点在圆上， . ②

将①代入②，得，于是既在圆上，又在圆上，从而圆与圆有公共点， ，解得，因此，实数的取值范围是.