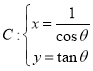题目内容
【题目】已知函数![]() .
.
(1)若曲线![]() 在点
在点![]() 处与直线
处与直线![]() 相切,求
相切,求![]() 的值;
的值;
(2)若函数![]() 有两个零点
有两个零点![]() ,试判断
,试判断![]() 的符号,并证明.
的符号,并证明.
【答案】(1) ![]() ;(2) 当
;(2) 当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
【解析】
试题分析:(1)求函数![]() 的导数
的导数![]() ,由
,由![]() 可求
可求![]() 的值;(2)由(1)可知
的值;(2)由(1)可知![]() ,且定义域为
,且定义域为![]() ,先讨论当
,先讨论当![]() 时
时![]() 的零点是否符合题意,当
的零点是否符合题意,当![]() 时,由
时,由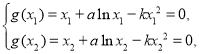 ,两式作差并整理得
,两式作差并整理得![]() ,则
,则![]() ,设
,设![]() ,
,![]() ,
,![]() ,,所以有
,,所以有![]() ,构造函数
,构造函数![]() ,讨论函数
,讨论函数![]() 的单调性与符号,可知
的单调性与符号,可知![]() 的符号.
的符号.
试题解析: (1)![]() ,又∵
,又∵![]() .………………2分
.………………2分
所以![]() .………………3分
.………………3分
(2)函数![]() 的定义域是
的定义域是![]() .………………4分
.………………4分
若![]() ,则
,则![]() .
.
令![]() ,则
,则![]() .
.
又据题设分析知![]() ,
,
∴![]() ,
,![]() .
.
又![]() 有两个零点,且都大于0,
有两个零点,且都大于0,
∴![]() ,不成立.………………5分
,不成立.………………5分
据题设知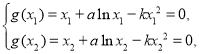
不妨设![]() ,
,![]() ,
,![]() .………………6分
.………………6分
所以![]() .
.
所以![]() .………………7分
.………………7分
又![]() ,
,
所以![]()
![]() .………………9分
.………………9分
引入![]() ,则
,则![]() .
.
所以![]() 在
在![]() 上单调递减.………………10分
上单调递减.………………10分
而![]() ,所以当
,所以当![]() 时,
时,![]() .
.
易知![]() ,
,![]() ,
,
所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .………………12分
.………………12分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目