题目内容
【题目】已知关于![]() 的二次函数
的二次函数![]() .
.
(1)设集合![]() 和
和![]() ,分别从集合
,分别从集合![]() 和
和![]() 中随机取一个数作为
中随机取一个数作为![]() 和
和![]() ,求函数
,求函数![]() 在区间
在区间![]() 上是增函数的概率;
上是增函数的概率;
(2)设点![]() 是区域
是区域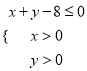 内的随机点,记事件“函数
内的随机点,记事件“函数![]() 有两个零点,其中一个大于1,另一个小于1”为事件
有两个零点,其中一个大于1,另一个小于1”为事件![]() ,求事件
,求事件![]() 发生的概率.
发生的概率.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)基本事件的总数有![]() 种,要函数在给定区间上单调递增,则需开口向上,且对称轴要小于或等于
种,要函数在给定区间上单调递增,则需开口向上,且对称轴要小于或等于![]() ,由此得到
,由此得到![]() 的大小关系,并通过列举得出符合题意的事件总数,利用古典概型计算公式计算得到概率.(2)“函数
的大小关系,并通过列举得出符合题意的事件总数,利用古典概型计算公式计算得到概率.(2)“函数![]() 有两个零点,其中一个大于1,另一个小于1”,由于函数开口向上,故只需
有两个零点,其中一个大于1,另一个小于1”,由于函数开口向上,故只需![]() ,画出可行域及符合题意的范围,利用面积比得到所求的概率.
,画出可行域及符合题意的范围,利用面积比得到所求的概率.
试题解析:
(1)记“函数![]() 在区间
在区间![]() 上是增函数”为事件
上是增函数”为事件![]() .
.
若使事件![]() 发生,由于
发生,由于![]() ,则只需使得
,则只需使得![]() ,即
,即![]() .
.
所以,事件![]() 包含的基本事件
包含的基本事件![]() 分别为
分别为![]() ,共5个;
,共5个;
所有基本事件共![]() 个.
个.
由古典概型的概率计算公式得, ![]() ,
,
综上,函数![]() 在区间
在区间![]() 上是增函数的概率为
上是增函数的概率为![]() ;
;
(2)若使事件![]() 发生,由于
发生,由于![]() ,所以只需
,所以只需![]() ,
,
所有结果构成的平面区域为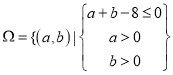 ,事件
,事件![]() 包含的结果构成的平面区域为
包含的结果构成的平面区域为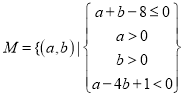 ,
,
如图所示:
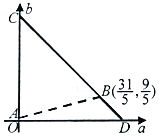
由几何概型的概率计算公式得, 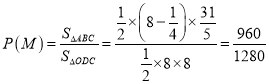 .
.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目