题目内容
【题目】函数![]() .
.
(1)若函数![]() 在
在![]() 上为增函数,求
上为增函数,求![]() 的取值范围;
的取值范围;
(2)若函数![]() 在
在![]() 上不单调时;
上不单调时;
①记![]() 在
在![]() 上的最大值、最小值分别为
上的最大值、最小值分别为![]() ,求
,求![]() ;
;
②设![]() ,若
,若![]() ,对
,对![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)①
(2)①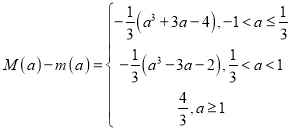 ②
②![]()
【解析】
试题分析:(1)先转化:分段函数![]() 在
在![]() 上为增函数,各段都为增函数且在结合点处(本题连续,不需讨论)也单调递增,因此只需在
上为增函数,各段都为增函数且在结合点处(本题连续,不需讨论)也单调递增,因此只需在![]() 为增函数,所以
为增函数,所以![]() (2)①先根据函数
(2)①先根据函数![]() 在
在![]() 上不单调,得
上不单调,得![]() ,而此时函数为先增再减再增,即在
,而此时函数为先增再减再增,即在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,因此根据定义区间
上是增函数,因此根据定义区间![]() 与单调区间位置关系分类讨论,确定最值,最后列出函数解析式②先转化不等式恒成立:由
与单调区间位置关系分类讨论,确定最值,最后列出函数解析式②先转化不等式恒成立:由![]() 得
得![]() ,所以
,所以![]() ,对
,对![]() 恒成立,等价于
恒成立,等价于![]() 在
在![]() 上的值域是
上的值域是![]() 的子集,由①中最值情况可得满足条件:当
的子集,由①中最值情况可得满足条件:当![]() 时,
时,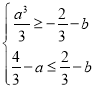 ,当
,当![]() 时,
时,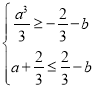 ,当
,当![]() 时,
时,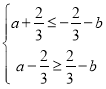 ,再研究对应函数
,再研究对应函数![]() 的取值范围,最后求并集得结果
的取值范围,最后求并集得结果
试题解析:由已知得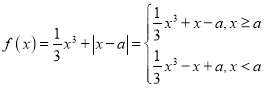 ,.............1分
,.............1分
令![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 上为增函数;.........2 分
上为增函数;.........2 分
令![]() ,则
,则![]() ,
,
令![]() ,得
,得![]() ,所以
,所以![]() 在
在![]() 和
和![]() 上是增函数,
上是增函数,
在![]() 上为减函数...................... 3分
上为减函数...................... 3分
(1)因为![]() 在
在![]() 上是增函数,所以
上是增函数,所以![]() 在
在![]() 为增函数,所以
为增函数,所以![]() ............4分
............4分
(2)因为函数![]() 在
在![]() 上不单调,所以
上不单调,所以![]() ,
,
①当![]() 时,
时,![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,
上是增函数,
所以![]() ............5分
............5分
当![]() ,即
,即![]() 时,
时,![]() ,
,
![]() ;........................6分
;........................6分
当![]() ,即
,即![]() 时,
时,![]() ,
,
![]() ;...........................7分
;...........................7分
当![]() 时,
时,![]() 在
在![]() 上是减函数,
上是减函数,
所以![]() ,故
,故![]() ,
,
综上得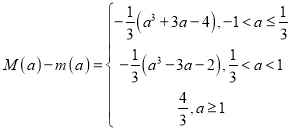 .......................8分
.......................8分
②![]() 对
对![]() 恒成立,即
恒成立,即![]() 在
在![]() 上的值域是
上的值域是![]() 的子集,
的子集,
当![]() 时,
时,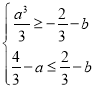 ,即
,即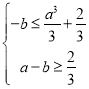 ,所以
,所以![]() ,
,
令![]() ,易得
,易得![]() 在
在![]() 上是增函数,
上是增函数,
则![]() ,所以
,所以![]() ..........................10分
..........................10分
当![]() 时,
时,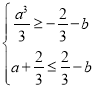 ,即
,即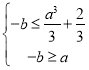 ,所以
,所以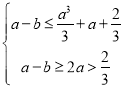 ,
,
令![]() ,易得
,易得![]() 在
在![]() 上是增函数,
上是增函数,
则![]() ,所以
,所以![]() ....................11分
....................11分
当![]() 时,
时,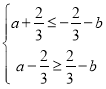 ,即
,即![]() ,即
,即![]() ,
,
所以![]() ,所以
,所以![]() ,综上得
,综上得![]() .............12分
.............12分

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案