题目内容
【题目】一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(1)从袋中随机取出两个球,求取出的球的编号之和不大于4的概率.
(2)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,求n<m+2的概率.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:
(1)从袋中随机抽取两个球,可能的结果有6种,而取出的球的编号之和不大于4的事件有两个,1和2,1和3,两种情况,求比值得到结果.
(2)有放回的取球,根据分步计数原理可知有16种结果,满足条件的比较多不好列举,可以首先考虑它的对立事件再来计算它的概率.
试题解析:
(1)从袋子中随机取两个球,其一切可能的结果组成的基本事件有1和2,1和3,1和4,2和3,2和4,3和4,共6个,从袋中随机取出的球的编号之和不大于4的事件共有1和2,1和3两个.
因此所求事件的概率为![]() .
.
(2)先从袋中随机取一个球,记下编号为m,放回后,在从袋中随机取一个球,记下编号为n,其中一切可能的结果(m,n)有:(1,1)(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1)(3, 2),(3,3)(3,4),(4,1),(4,2),(4,3),(4,4),共16个.
所有满足条件n≥m+2的事件为(1,3)(1,4)(2,4),共3个,
所以满足条件n≥m+2的事件的概率为P1=![]() .
.
故满足条件n<m+2的事件的概率为1-P1=1-![]() =
=![]() .
.

 53随堂测系列答案
53随堂测系列答案【题目】“真人秀”热潮在我国愈演愈烈,为了了解学生是否喜欢某“真人秀”节目,在某中学随机调查了110名学生,得到如下列联表:
男 | 女 | 总计 | |
喜欢 | 40 | 20 | 60 |
不喜欢 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由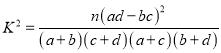 算得
算得![]() .
.
附表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
参照附表,得到的正确结论是( )
A. 在犯错误的概率不超过![]() 的前提下,认为“喜欢该节目与性别有关”
的前提下,认为“喜欢该节目与性别有关”
B. 在犯错误的概率不超过![]() 的前提下,认为“喜欢该节目与性别无关”
的前提下,认为“喜欢该节目与性别无关”
C. 有![]() 以上的把握认为“喜欢该节目与性别有关”
以上的把握认为“喜欢该节目与性别有关”
D. 有