题目内容
曲线f(x)=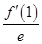 ·ex-f(0)x+
·ex-f(0)x+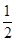 x2在点(1,f(1))处的切线方程为____________.
x2在点(1,f(1))处的切线方程为____________.
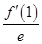 ·ex-f(0)x+
·ex-f(0)x+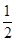 x2在点(1,f(1))处的切线方程为____________.
x2在点(1,f(1))处的切线方程为____________.y=ex-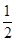
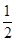
因为f′(x)=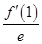 ·ex-f(0)+x,故有
·ex-f(0)+x,故有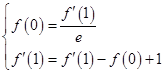
即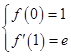 原函数表达式可化为f(x)=ex-x+
原函数表达式可化为f(x)=ex-x+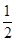 x2,从而f(1)=e-
x2,从而f(1)=e-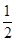 ,所以所求切线方程为y-
,所以所求切线方程为y-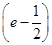 =e(x-1),
=e(x-1),
即y=ex-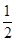 .
.
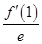 ·ex-f(0)+x,故有
·ex-f(0)+x,故有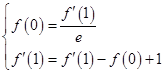
即
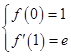 原函数表达式可化为f(x)=ex-x+
原函数表达式可化为f(x)=ex-x+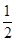 x2,从而f(1)=e-
x2,从而f(1)=e-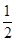 ,所以所求切线方程为y-
,所以所求切线方程为y-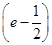 =e(x-1),
=e(x-1),即y=ex-
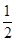 .
.
练习册系列答案
相关题目
 (m为实数).
(m为实数). ),f(
),f(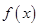 满足如下条件:当
满足如下条件:当 时,
时,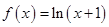 ,且对任
,且对任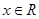 ,都有
,都有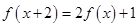 .
.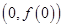 处的切线方程;
处的切线方程;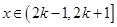 ,
,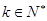 时,函数
时,函数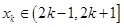 ,
,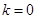 、
、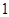 、
、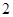 、
、 、
、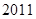 ,使得等式
,使得等式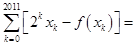
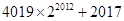 成立?若存在就求出
成立?若存在就求出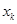 (
(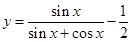 在点
在点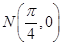 处的切线的斜率为 .
处的切线的斜率为 .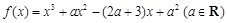 .
.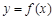 在
在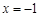 处的切线与直线
处的切线与直线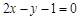 平行,求a的值;
平行,求a的值;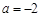 时,求
时,求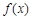 的单调区间.
的单调区间. 上过点(1,0)的切线方程( )
上过点(1,0)的切线方程( )



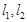 是曲线
是曲线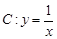 的两条互相平行的切线,则
的两条互相平行的切线,则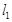 与
与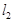 的距离的最大值为_____.
的距离的最大值为_____.