题目内容
已知函数f(x)=sinx,g(x)=mx- (m为实数).
(m为实数).
(1)求曲线y=f(x)在点P( ),f(
),f( )处的切线方程;
)处的切线方程;
(2)求函数g(x)的单调递减区间;
(3)若m=1,证明:当x>0时,f(x)<g(x)+ .
.
 (m为实数).
(m为实数).(1)求曲线y=f(x)在点P(
 ),f(
),f( )处的切线方程;
)处的切线方程;(2)求函数g(x)的单调递减区间;
(3)若m=1,证明:当x>0时,f(x)<g(x)+
 .
.(1)x-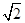 y+1-
y+1- =0
=0
(2)则g(x)的单调递减区间是(-∞,- ),(
),( ,+∞).
,+∞).
(3)见解析
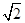 y+1-
y+1- =0
=0(2)则g(x)的单调递减区间是(-∞,-
 ),(
),( ,+∞).
,+∞).(3)见解析
解:(1)由题意得所求切线的斜率k=f′( )=cos
)=cos =
=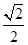 .
.
切点P( ,
,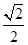 ),则切线方程为y-
),则切线方程为y-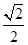 =
=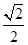 (x-
(x- ),
),
即x-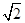 y+1-
y+1- =0.
=0.
(2)g′(x)=m-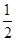 x2.
x2.
①当m≤0时,g′(x)≤0,则g(x)的单调递减区间是(-∞,+∞);
②当m>0时,令g′(x)<0,解得x<- 或x>
或x> ,
,
则g(x)的单调递减区间是(-∞,- ),(
),( ,+∞).
,+∞).
(3)证明:当m=1时,g(x)=x- .
.
令h(x)=x-sinx,x∈[0,+∞),h′(x)=1-cosx≥0,
则h(x)是[0,+∞)上的增函数.
故当x>0时,h(x)>h(0)=0,即sinx<x,f(x)<g(x)+ .
.
 )=cos
)=cos =
=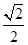 .
.切点P(
 ,
,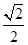 ),则切线方程为y-
),则切线方程为y-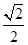 =
=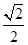 (x-
(x- ),
),即x-
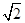 y+1-
y+1- =0.
=0.(2)g′(x)=m-
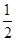 x2.
x2.①当m≤0时,g′(x)≤0,则g(x)的单调递减区间是(-∞,+∞);
②当m>0时,令g′(x)<0,解得x<-
 或x>
或x> ,
,则g(x)的单调递减区间是(-∞,-
 ),(
),( ,+∞).
,+∞).(3)证明:当m=1时,g(x)=x-
 .
.令h(x)=x-sinx,x∈[0,+∞),h′(x)=1-cosx≥0,
则h(x)是[0,+∞)上的增函数.
故当x>0时,h(x)>h(0)=0,即sinx<x,f(x)<g(x)+
 .
.
练习册系列答案
相关题目
 在R上可导,且满足
在R上可导,且满足 ,则
,则
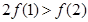

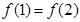
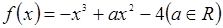 .
.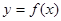 的图象在点
的图象在点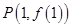 处的切线的倾斜角为
处的切线的倾斜角为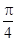 ,求
,求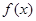 在
在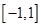 上的最小值;
上的最小值;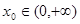 ,使
,使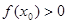 ,求a的取值范围.
,求a的取值范围.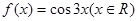 ,则曲线
,则曲线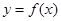 在
在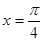 处的切线的斜率为( )
处的切线的斜率为( )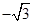
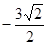
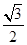
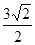
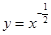 在点
在点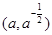 处的切线与两坐标轴围成的三角形面积为18.则
处的切线与两坐标轴围成的三角形面积为18.则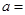 ( )
( )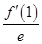 ·ex-f(0)x+
·ex-f(0)x+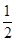 x2在点(1,f(1))处的切线方程为____________.
x2在点(1,f(1))处的切线方程为____________. (
( ),其中
),其中 自然对数的底数。
自然对数的底数。 处的切线方程为
处的切线方程为 ,求
,求 的值;
的值; 的单调区间;
的单调区间; ,当
,当 时,存在
时,存在 使得
使得 成立,求
成立,求 的取值范围.
的取值范围.