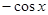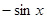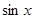题目内容
已知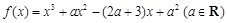 .
.
(1)若曲线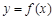 在
在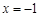 处的切线与直线
处的切线与直线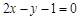 平行,求a的值;
平行,求a的值;
(2)当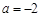 时,求
时,求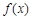 的单调区间.
的单调区间.
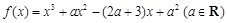 .
.(1)若曲线
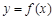 在
在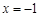 处的切线与直线
处的切线与直线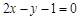 平行,求a的值;
平行,求a的值;(2)当
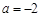 时,求
时,求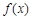 的单调区间.
的单调区间.(1)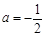 ;(2)
;(2)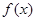 单调递增区间为
单调递增区间为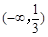 ,
,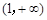 ;单调递减区间为
;单调递减区间为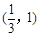
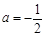 ;(2)
;(2)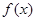 单调递增区间为
单调递增区间为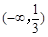 ,
,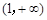 ;单调递减区间为
;单调递减区间为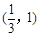
试题分析:(1)先求导,由直线方程可知此直线斜率为2,则曲线
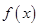 在
在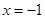 处的切线的斜率也为2.由导数的几何意义可知
处的切线的斜率也为2.由导数的几何意义可知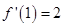 。即可得
。即可得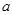 的值。(2)先求导,再令导数大于0得增区间,令导数小于0得减区间。
的值。(2)先求导,再令导数大于0得增区间,令导数小于0得减区间。(1) 由题意得
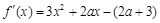 时
时∴

∴
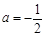 6分
6分(2) ∵
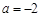 ,∴
,∴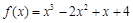
∴
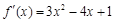 ,令
,令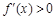 ,得
,得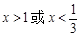
令
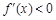 ,得
,得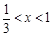
∴
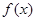 单调递增区间为
单调递增区间为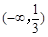 ,
,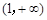
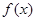 单调递减区间为
单调递减区间为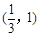 13分
13分
练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
 .
.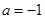 时,求
时,求 在
在 处的切线方程;
处的切线方程; ,
, 有且仅有一个零点时,求
有且仅有一个零点时,求 的值;
的值; ,
, ,求
,求 的取值范围.
的取值范围.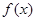 与
与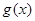 都是定义在R上的函数,
都是定义在R上的函数,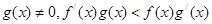 ,且
,且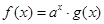
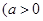 ,且
,且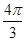 ,在有穷数列
,在有穷数列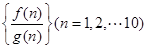 中,任意取前
中,任意取前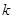 项相加,则前
项相加,则前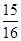 的概率是( )
的概率是( )


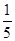
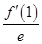 ·ex-f(0)x+
·ex-f(0)x+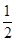 x2在点(1,f(1))处的切线方程为____________.
x2在点(1,f(1))处的切线方程为____________. 在点
在点 处的切线方程为 .
处的切线方程为 . 的图象记为E.过点
的图象记为E.过点 作曲线E的切线,这样的切线有且仅有两条,求
作曲线E的切线,这样的切线有且仅有两条,求 的值.
的值. ,
,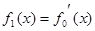 ,
,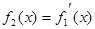 ,……,
,……,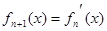 ,
,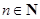 ,则
,则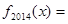 ( )
( )