题目内容
【题目】甲船在点
发现乙船在北偏东
的
处，
里，且乙船以每小时10里的速度向正北行驶，已知甲船的速度是每小时
里，问：甲船以什么方向前进，才能与乙船最快相遇，相遇时甲船行驶了多少小时？
【答案】甲船应朝北偏东30°方向行驶，才能与乙船最快相遇，相遇时甲船行驶了2小时．
【解析】
构建两个直角三角形后，在RT△ABD，可求出AD，BD，设
，在RT△ACD中运用勾股定理可求出
，从而求出∠CAD，则可找到甲船所行驶方向，进而求出相遇时的时间．
解：如图，设甲船在C处追上乙船，延长CB与东西方向交与点D，根据题意知CD⊥AD，
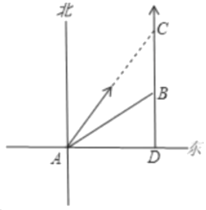
∴∠ADB＝90°，∠BAD＝30°，
∴BD=10，
由勾股定理得：AD＝
，
∵乙船正以每小时10海里的速度向正北方向行驶，而甲船的速度是海里/小时，
∴设，则AC＝
，
又在
中，
，
解得
或
（舍），
此时AC＝
，
，
所以
，
相遇时甲船行驶了
小时，
∴甲船应朝北偏东30°方向行驶，才能与乙船最快相遇，相遇时甲船行驶了2小时，
故答案为：甲船应朝北偏东30°方向行驶，才能与乙船最快相遇，相遇时甲船行驶了2小时．
练习册系列答案
相关题目
【题目】某同学用“五点法”画函数
，在某一周期内的图象时，列表并填入了部分数据，如下表：
| 0 |
|
|
|
|
x |
|
| |||
| 0 | 2 | 0 | 0 |
（1）请将上表数据补充完整，并求函数
的解析式；
（2）求函数的单调递增区间；
（3）求函数在区间
上的最大值和最小值.
