题目内容
已知f(x)=-x2+2x,x∈[-1,2],则f(x)的值域为 .
考点:二次函数在闭区间上的最值
专题:函数的性质及应用
分析:根据f(x)=-(x-1)2+1,x∈[-1,2],利用二次函数的性质求得f(x)的值域.
解答:
解:∵f(x)=-x2+2x=-(x-1)2+1,x∈[-1,2],故当x=1时,函数取得最大值为1;
当x=-1时,函数取得最小值为-3,
故函数的值域为[-3,1],
故答案为:[-3,1].
当x=-1时,函数取得最小值为-3,
故函数的值域为[-3,1],
故答案为:[-3,1].
点评:本题主要考查求二次函数在闭区间上的最值,二次函数的性质的应用,属基础题.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
已知函数f(x)在R上可导,其导函数为f′(x),若f′(x)满足
>0,y=
关于直线x=1对称,则不等式
<f(0)的解集是( )
| f′(x)-f(x) |
| x-1 |
| f(x) |
| ex |
| f(x2-x) |
| ex2-x |
| A、(-1,2) |
| B、(1,2) |
| C、(-1,0)∪(1,2) |
| D、(-∞,0)∪(1,+∞) |
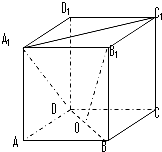
 如图,四棱锥P-ABCD中,PB⊥底面ABCD,CD⊥PD,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3,点E在棱PA上,且PE=2EA.
如图,四棱锥P-ABCD中,PB⊥底面ABCD,CD⊥PD,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3,点E在棱PA上,且PE=2EA.