题目内容
已知定义在R上函数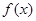 是偶函数,对
是偶函数,对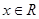 都有
都有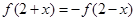 ,当
,当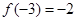 时f (2013)的值为 .
时f (2013)的值为 .
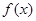 是偶函数,对
是偶函数,对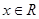 都有
都有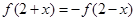 ,当
,当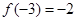 时f (2013)的值为 .
时f (2013)的值为 .-2
试题分析:根据题意,由于定义在R上函数
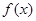 是偶函数,对
是偶函数,对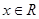 都有
都有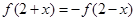 ,那么可知f(4+x)=-f(x),发(8+x)=f(x),可知周期为8,那么对于2013=
,那么可知f(4+x)=-f(x),发(8+x)=f(x),可知周期为8,那么对于2013=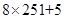 ,f (2013)=f()=f(-3)=-2,故可知答案为-2.
,f (2013)=f()=f(-3)=-2,故可知答案为-2.点评:主要是考查了抽象函数周期性的运用,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
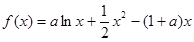
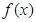 的单调区间;
的单调区间;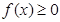 对定义域内的任意的
对定义域内的任意的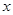 恒成立,求实数
恒成立,求实数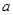 的取值范围.
的取值范围.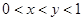 ,则( )
,则( )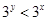
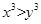

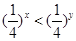
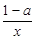 -1.
-1. 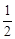 时, 求函数f(x)的单调区间;
时, 求函数f(x)的单调区间;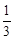 时, 设函数g(x)=x2-2bx-
时, 设函数g(x)=x2-2bx-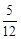 , 若对于
, 若对于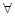 x1∈
x1∈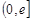 ,
, 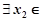 [0, 1]使f(x1)≥g(x2)成立, 求实数b的取值范围.(e是自然对数的底, e<
[0, 1]使f(x1)≥g(x2)成立, 求实数b的取值范围.(e是自然对数的底, e<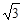 +1).
+1). 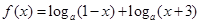 ,其中
,其中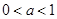 ,记函数
,记函数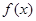 的定义域为D.
的定义域为D.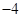 ,求
,求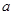 的值;
的值;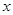 ,不等式
,不等式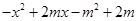 <
<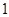 恒成立,求实数
恒成立,求实数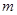 的取值范围.
的取值范围.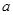 ,
,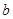 为正实数,函数
为正实数,函数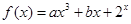 在
在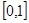 上的最大值为
上的最大值为 ,则
,则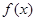 在
在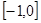 上的最小值为 .
上的最小值为 .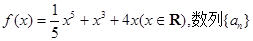 是等差数列,
是等差数列,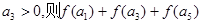 的值
的值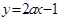 在[0,2]上的最大值是7,则指数函数
在[0,2]上的最大值是7,则指数函数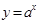 在[0,2]上的最大值与最小值的和为
在[0,2]上的最大值与最小值的和为