题目内容
(本小题满分14分)
已知a、b、c是△ABC中A、B、C的对边, 关于x的方程b (x 2 + 1 ) + c (x 2– 1 ) –2ax =" 0" 有两个相等的实根, 且sinCcosA – cosCsinA="0," 试判定△ABC的形状.
已知a、b、c是△ABC中A、B、C的对边, 关于x的方程b (x 2 + 1 ) + c (x 2– 1 ) –2ax =" 0" 有两个相等的实根, 且sinCcosA – cosCsinA="0," 试判定△ABC的形状.
等腰直角三角形
∵(b + c)x 2 –2ax + (b – c ) = 0有相等实根,
∴⊿=" 4a" 2 – 4( b + c )(b – c) = 0, 3分
∴ a 2 + c 2 – b 2 = 0,
∴ B = 90° . 3分
又sinCcosA – cosCsinA="0" ,
得 sin (C – A) =" 0," 3分
∵–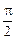 < C – A <
< C – A < 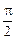 . 2分
. 2分
∴ A = C.
∴△ABC是B为直角的等腰直角三角形. 3分
∴⊿=" 4a" 2 – 4( b + c )(b – c) = 0, 3分
∴ a 2 + c 2 – b 2 = 0,
∴ B = 90° . 3分
又sinCcosA – cosCsinA="0" ,
得 sin (C – A) =" 0," 3分
∵–
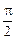 < C – A <
< C – A < 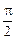 . 2分
. 2分∴ A = C.
∴△ABC是B为直角的等腰直角三角形. 3分

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
 中,角A,B,C的对边长分别为
中,角A,B,C的对边长分别为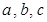 ,
, ,则
,则
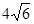
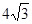
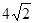
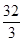
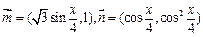 .
.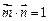 ,求
,求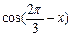 的值;
的值;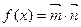 ,在△ABC中,角
,在△ABC中,角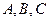 的对边分别是
的对边分别是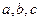 且满足
且满足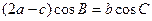 ,求函数f(A)的取值范围.
,求函数f(A)的取值范围.  中,内角
中,内角 对边的边长分别是
对边的边长分别是 ,且
,且 ,
, (2)若边
(2)若边 且
且 ,求
,求 的值.(12分)
的值.(12分)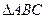 中,
中,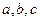 分别是
分别是 的对边长,已知
的对边长,已知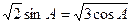 .
. 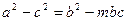 ,求实数
,求实数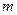 的值;
的值; 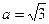 ,求
,求 ,则
,则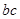 的最大值是 .
的最大值是 .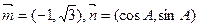 ,且
,且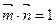 .
.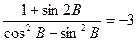 ,求
,求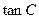 .
. .
.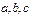 ,若
,若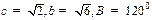 ,则
,则