题目内容
【题目】数列{an}满足an=2an﹣1+2n+1(n∈N* , n≥2),a3=27.
(1)求a1 , a2的值;
(2)是否存在一个实数t,使得bn= ![]() (an+t)(n∈N*),且数列{bn}为等差数列?若存在,求出实数t;若不存在,请说明理由;
(an+t)(n∈N*),且数列{bn}为等差数列?若存在,求出实数t;若不存在,请说明理由;
(3)求数列{an}的前n项和Sn .
【答案】
(1)解:由a3=27,27=2a2+23+1,
∴a2=9,
∴9=2a1+22+1∴a1=2
(2)解:假设存在实数t,使得{bn}为等差数列.
则2bn=bn﹣1+bn+1,
∴ ![]()
∴4an=4an﹣1+an+1+t,
∴ ![]() ∴t=1,
∴t=1,
存在t=1,使得数列{bn}为等差数列
(3)解:由(1)、(2)知: ![]() ,
,
又{bn}为等差数列. ![]() ∴
∴ ![]() ,
,
∴Sn=3×20﹣1+5×21﹣1+7×22﹣1+…+(2n+1)×2n﹣1﹣1=3+5×2+7×22+…+(2n+1)×2n﹣1﹣n
∴2Sn=3×2+5×22+7×23+…+(2n+1)×2n﹣2n∴﹣Sn=3+2×2+2×22+2×23+…+2×2n﹣1﹣(2n+1)×2n+n
= ![]()
=(1﹣2n)×2n+n﹣1Sn=(2n﹣1)×2n﹣n+1
【解析】(Ⅰ)利用an=2an﹣1+2n+1(n∈N,n≥2),a3=27,代入可求;(Ⅱ)假设存在实数t,使得{bn}为等差数列,从而有2bn=bn﹣1+bn+1 , .故可求;(Ⅲ)先求出数列的通项 ![]() ,再求和.
,再求和.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系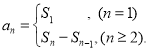 ,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目