题目内容
【题目】已知函数
．
（1）若不等式
恒成立，求实数
的最大值；
（2）当
时，函数
有零点，求实数
的取值范围．
【答案】（1） 1 ； （2） (-
, -
]
【解析】
(1)利用绝对值三角不等式得到|x-a|-|x+m-a|
|m|≤1，即得实数m的最大值.(2)先化简函数g(x)得到分段函数，再根据分段函数的图像有零点得到实数a的取值范围.
（1）因为 f(x)=|x-a|+3a, 所以f(x+m)=|x+m-a|+3a
所以 f(x)- f(x+m)= |x-a|-|x+m-a||m|
因为不等式f(x)- f(x+m)1 恒成立，所以|m|1
解得 -1m
故实数 m 的最大值为 1 ．
（2）当a
时，g(x)=f(x)+|2x-1|=|x-a|+|2x-1|+3a=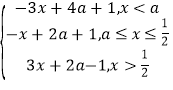
所以g(x)min=g(
)=+2a0 .
解得a
.
故实数 a 的取值范围是(-, －]
【题目】某商场销售某种品牌的空调器，每周周初购进一定数量的空调器，商场每销售一台空调器可获利500元，若供大于求，则每台多余的空调器需交保管费100元；若供不应求，则可从其他商店调剂供应，此时每台空调器仅获利润200元．
（Ⅰ）若该商场周初购进20台空调器，求当周的利润（单位：元）关于当周需求量n（单位：台，n∈N）的函数解析式f（n）；
（Ⅱ）该商场记录了去年夏天（共10周）空调器需求量n（单位：台），整理得表：
周需求量n | 18 | 19 | 20 | 21 | 22 |
频数 | 1 | 2 | 3 | 3 | 1 |
以10周记录的各需求量的频率作为各需求量发生的概率，若商场周初购进20台空调器，X表示当周的利润（单位：元），求X的分布列及数学期望．
【题目】随着资本市场的强势进入，互联网共享单车“忽如一夜春风来”，遍布了各个城市的大街小巷．为了解共享单车在
市的使用情况，某调研机构在该市随机抽取了
位市民进行调查，得到的
列联表如下：
经常使用 | 偶尔或不用 | 合计 | |
|
|
|
|
|
|
|
|
合计 |
|
|
|
（1）根据以上数据，能否在犯错误的概率不超过
的前提下认为使用共享单车的情况与年龄有关？
（2）现从所抽取的
岁以上的市民中利用分层抽样的方法再抽取
位市民，从这位市民中随机选出
位市民赠送礼品，求选出的位市民中至少有
位市民经常使用共享单车的概率．
参考公式及数据：
，
．
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
