题目内容
【题目】已知f(x)=x2﹣a|x﹣1|+b(a>0,b>﹣1)
(1)若b=0,a>2,求f(x)在区间[0,2]内的最小值m(a);
(2)若f(x)在区间[0,2]内不同的零点恰有两个,且落在区间[0,1),(1,2]内各一个,求a﹣b的取值范围.
【答案】
(1)解:b=0,a>2时,f(x)=x2﹣a|x﹣1|,
当0≤x≤1时,f(x)=x2+ax﹣a,且在[0,1]递增,
可得f(0)取得最小值﹣a;
当1<x≤2时,f(x)=x2﹣ax+a, ![]() >1,
>1,
当a>4时, ![]() >2,在(1,2]递减,可得最小值f(2)=4﹣a;
>2,在(1,2]递减,可得最小值f(2)=4﹣a;
当2<a≤4时,1< ![]() ≤2,可得f(
≤2,可得f( ![]() )取得最小值,且为a﹣
)取得最小值,且为a﹣ ![]() .
.
由﹣a<4﹣a,a﹣ ![]() ﹣(﹣a)=
﹣(﹣a)= ![]() >0(2<a≤4),
>0(2<a≤4),
即有a﹣ ![]() >﹣a.
>﹣a.
综上可得,m(a)=﹣a;
(2)解:由f(x)= ![]() ,
,
当0≤x<1时,f(x)递增,可得f(0)f(1)≤0,
即为(b﹣a)(1+b)≤0①
当1<x≤2时,f(x)有一个零点,可得f(1)f(2)≤0或f( ![]() )=0(2<a≤4),
)=0(2<a≤4),
即为(1+b)(4﹣a+b)≤0或b= ![]() ﹣a②
﹣a②
由 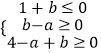 或
或 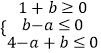 或a﹣b=
或a﹣b= ![]() (2<a≤4),
(2<a≤4),
可得a﹣b≤0或a﹣b≥4或3<a﹣b≤4,
综上可得a﹣b的范围是(﹣∞,0]∪(3,+∞)
【解析】(1)讨论当0≤x≤1时,当1<x≤2时,同时对a讨论,可得f(x)的单调性,可得最小值;(2)将f(x)写成分段函数式,讨论当0≤x<1时,当1<x≤2时,由函数的零点存在定理,可得不等式组,解不等式即可得到所求范围.
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识,掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减.
上递减.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案【题目】为了解学生的课外阅读时间情况,某学校随机抽取了50人进行统计分析,把这50人每天阅读的时间(单位:分钟)绘制成频数分布表,如下表所示:
阅读时间 | [0,20) | [20,40) | [40,60) | [60,80) | [80,100) | [100,120] |
人数 | 8 | 10 | 12 | 11 | 7 | 2 |
若把每天阅读时间在60分钟以上(含60分钟)的同学称为“阅读达人”,根据统计结果中男女生阅读达人的数据,制作出如图所示的等高条形图.

(1)根据抽样结果估计该校学生的每天平均阅读时间(同一组数据用该区间的中点值作为代表);
(2)根据已知条件完成下面的2×2列联表,并判断是否有99%的把握认为“阅读达人”跟性别有关?
男生 | 女生 | 总计 | |
阅读达人 | |||
非阅读达人 | |||
总计 |
附:参考公式![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
临界值表:
P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |