题目内容
11.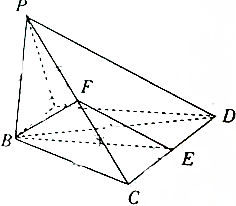 如图,在四棱锥P-ABCD中,AB⊥PA,AB∥CD,且PB=BC=BD=$\sqrt{6}$,CD=2AB=2$\sqrt{2}$,∠PAD=120°,E和F分别是侧棱CD和PC的中点.
如图,在四棱锥P-ABCD中,AB⊥PA,AB∥CD,且PB=BC=BD=$\sqrt{6}$,CD=2AB=2$\sqrt{2}$,∠PAD=120°,E和F分别是侧棱CD和PC的中点.(1)求证:平面BEF⊥平面PCD;
(2)求三棱锥F-BCE的体积.
分析 (1)证明平面BEF⊥平面PCD,可证CD⊥平面BEF,由已知可得CD⊥BE,然后证明CD⊥EF,又BE∩EF=E,可得CD⊥面BEF,则平面BEF⊥平面PCD;
(2)由(1)知,CE⊥平面BEF,把三棱锥F-BCE的体积利用等积法转化为求C-BFE的体积,通过解三角形求得三角形BFE为直角三角形且求得边长,代入体积公式得答案.
解答 (1)证明:如图,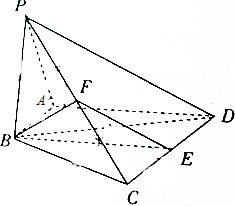 ∵AB⊥PA,AB∥CD,∴CD⊥PA,
∵AB⊥PA,AB∥CD,∴CD⊥PA,
∵BC=CD,E为CD中点,∴CD⊥BE,
∵AB∥CD,AB=$\frac{1}{2}CD$=ED,∴四边形ABED为平行四边形,则BE∥AD,
∴CD⊥AD,又PA∩AD=A,
∴CD⊥面PAD,则CD⊥PD,
∵E,F分别为CD,PC中点,∴EF∥PD,
则CD⊥EF,又BE∩EF=E,
∴CD⊥面BEF,
∴平面BEF⊥平面PCD;
(2)解:由(1)知,CE⊥平面BEF,
在等腰三角形BCD中,底边上的高BE=$\sqrt{B{C}^{2}-C{E}^{2}}=\sqrt{6-2}=2$,
在直角三角形PAB中,PA=$\sqrt{P{B}^{2}-A{B}^{2}}=\sqrt{6-2}=2$,
在三角形PAD中,PD=$\sqrt{P{A}^{2}+A{D}^{2}-2PA•AD•cos120°}$=$\sqrt{{2}^{2}+{2}^{2}-2×2×2×(-\frac{1}{2})}=2\sqrt{3}$.
则EF=$\sqrt{3}$,
PC=$\sqrt{(2\sqrt{3})^{2}+(2\sqrt{2})^{2}}=2\sqrt{5}$,则BF=$\sqrt{(\sqrt{6})^{2}-(\sqrt{5})^{2}}=1$,
在三角形BEF中,由BE=2,EF=$\sqrt{3}$,BF=1,可得∠BFE=90°,
∴VF-BCE=VC-BFE=$\frac{1}{3}×\frac{1}{2}×\sqrt{3}×1×\sqrt{2}=\frac{\sqrt{6}}{6}$.
点评 本小题主要考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力,是中档题.

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案| A. | 向左平移$\frac{π}{8}$个单位得到 | B. | 向右平移$\frac{π}{8}$个单位得到 | ||
| C. | 向左平移$\frac{π}{4}$个单位得到 | D. | 向左右平移$\frac{π}{4}$个单位得到 |