题目内容

1．已知x＞0，y＞0，$\frac{4}{x}$+$\frac{1}{y}$=$\frac{1}{2}$，则x+y的最小值为（　　）
A．61B．16C．81D．18

分析 变形x+y=2（$\frac{4}{x}$+$\frac{1}{y}$）（x+y）=10+$\frac{2x}{y}$$+\frac{8y}{x}$利用基本不等式求解即可．．

解答 解：∵x＞0，y＞0，$\frac{4}{x}$+$\frac{1}{y}$=$\frac{1}{2}$，
则x+y=2（$\frac{4}{x}$+$\frac{1}{y}$）（x+y）=10+$\frac{2x}{y}$$+\frac{8y}{x}$≥10+2$\sqrt{16}$=18，（$\frac{2x}{y}$=$\frac{8y}{x}$时等号成立，即x=12，y=6时等号成立）
故选：D

点评 本题主要考查了基本不等式在求解最值中的应用，解题的关键是进行1的代换，属于基础试题

练习册系列答案
相关题目
11．在平面直角坐标系中，曲线C1的参数方程为 $\left\{\begin{array}{l}{x=acosφ}\\{y=bsinφ}\end{array}\right.$（a＞b＞0，φ为参数），在以Ο为极点，x轴的正半轴为极轴的坐标系中，曲线C2是圆心在极轴上且经过极点的圆，已知曲线C1上的点M（$\sqrt{3}$，$\frac{1}{2}$）对应的参数φ=$\frac{π}{6}$，射线θ=$\frac{π}{3}$与曲线C2交于点D（1，$\frac{π}{3}$）．
（1）求曲线C1，C2的直角坐标方程；
（2）若点A（ρ1，θ），Β（ρ2，θ+$\frac{π}{2}$）都在曲线C1上，求$\frac{1}{{ρ}_{1}^{2}+{ρ}_{2}^{2}}$的值．
12．已知函数f（x）=ex-ax+a，其中a∈R，e为自然对数的底数．
（1）讨论函数f（x）的单调性，并写出对应的单调区间；
（2）设b∈R，若函数f（x）≥b对任意x∈R都成立，求ab的最大值．
9．求直线l1：y-2=0，l2：3x+2y-12=0的交点，并画图．
16．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的虚轴端点和实轴端点都在同一个圆上，过该双曲线的一个焦点作垂直于实轴的直线，则该直线被双曲线截得的弦长与焦距之比为（　　）
A．$\frac{1}{2}$B．$\frac{\sqrt{2}}{2}$C．2D．$\sqrt{2}$
6．若双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{8}$=1上任一点P到两焦点的距离的比为2：1，则点P到两焦点的距离之和为12．
13．下列说法中，错误的个数为（　　）
①向量$\overrightarrow{AB}$的长度与向量$\overrightarrow{BA}$的长度相等；
②若两个非零向量$\overrightarrow{a}$∥$\overrightarrow{b}$，则$\overrightarrow{a}$与$\overrightarrow{b}$的方向相同或相反；
③两个公共终点的向量一定是共线向量；
④共线向量是可以移动到同一条直线上的向量；
⑤平行向量就是向量所在的直线平行．
A．1B．2C．3D．4
10．已知P为$\frac{{x}^{2}}{4}$-y2=1上的一点，F1、F2为焦点，且∠F1PF2=60°，求S${\;}_{△{F}_{1}P{F}_{2}}$．
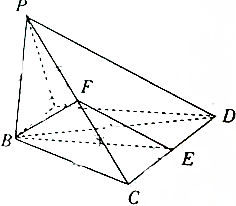11．如图，在四棱锥P-ABCD中，AB⊥PA，AB∥CD，且PB=BC=BD=$\sqrt{6}$，CD=2AB=2$\sqrt{2}$，∠PAD=120°，E和F分别是侧棱CD和PC的中点．
（1）求证：平面BEF⊥平面PCD；
（2）求三棱锥F-BCE的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网