题目内容
6．△ABC的顶点B，C坐标分别为（0，0），（a，0），AB边上的中线长为m，求点A的轨迹方程．分析 设出A点坐标，求得AB的中点坐标，然后由两点间的距离公式列式求得点A的轨迹方程．
解答 解：设A点坐标为（x，y），则AB的中点坐标为（$\frac{x}{2}，\frac{y}{2}$），
又C（a，0），根据两点间的距离公式，有
$\sqrt{（\frac{x}{2}-a）^{2}+（\frac{y}{2}）^{2}}=m$，
整理得：（x-2a）2+y2=4m2（y≠0）．
∴点A的轨迹方程为（x-2a）2+y2=4m2（y≠0）．
点评 本题考查了轨迹方程的求法，关键是去掉不合题意的点，是基础题．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
16．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的虚轴端点和实轴端点都在同一个圆上，过该双曲线的一个焦点作垂直于实轴的直线，则该直线被双曲线截得的弦长与焦距之比为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | 2 | D． | $\sqrt{2}$ |
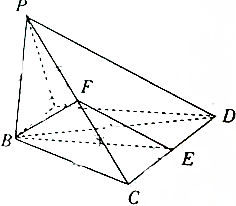如图，在四棱锥P-ABCD中，AB⊥PA，AB∥CD，且PB=BC=BD=$\sqrt{6}$，CD=2AB=2$\sqrt{2}$，∠PAD=120°，E和F分别是侧棱CD和PC的中点．